|
Match Editorial |
Saturday, October 16, 2004
Match summary
In division 1, coders had a pretty easy time with the easy and medium problems, but no one was able to get a tricky hard problem. As a result, the top scores were quite close going into the challenge phase. Not surprisingly, the results ended up being determined by challenges, and wleite was able to get 4 of them, to take first. kirkifer took second with 5 challenges, and AdrianKeugel was a distant third, with only one challenge. In division 2, coders had an easier time, as 40 coders solved the hard problem. 35C4P3 took first by a respectable margin, followed by first timer Rud0lf and Artist_ in second and third, respectively.
The Problems
DivisorDigits
Used as: Division Two - Level One:
Value 250 Submission Rate 216 / 226 (95.58%) Success Rate 194 / 216 (89.81%) High Score Sleeve for 249.19 points (1 mins 37 secs) Average Score 224.89 (for 194 correct submissions)
The key to this problem is to first represent the input integer as a string. Once that is complete, loop through each character and test for divisibility. Just be sure not to try 0, since your divisibility check may throw an exception.
Mailbox
Used as: Division Two - Level Two:
Value 500 Submission Rate 196 / 226 (86.73%) Success Rate 175 / 196 (89.29%) High Score Sleeve for 486.96 points (4 mins 40 secs) Average Score 378.67 (for 175 correct submissions)
For each address, we need to check and see if that address can be formed from the letters in the collection. There are a number of ways to do this. Perhaps the simplest is to write two nested loops, keeping track of which letters have been used from the collection:
bool[] used = new bool[collection.size()];
for(int i = 0; i<address.size(); i++){
bool found = false;
for(int j = 0; j<collection.size(); j++){
if(!used[j] && collection[j] == address[i]){
used[j] = true;
found = true;
break;
}
}
if(!found){
ret++;
break;
}
}
Another way to solve this, which has a faster runtime (unnecessary in this
case), is to sort both the characters in collection and the characters in
address:
sort(collection);
sort(address);
int ptr = 0;
for(int i = 0; i < collection.size(); i++){
if(ptr < address.size() && collection[i] == address[ptr]){
ptr++;
}
}
if(ptr!=address.size())ret++;
Thesaurus

Used as: Division Two - Level Three:
Used as: Division One - Level Two:
Value 1000 Submission Rate 65 / 226 (28.76%) Success Rate 40 / 65 (61.54%) High Score Javaholic for 801.56 points (14 mins 55 secs) Average Score 539.26 (for 40 correct submissions)
Value 500 Submission Rate 136 / 169 (80.47%) Success Rate 110 / 136 (80.88%) High Score Krzysan for 463.44 points (8 mins 6 secs) Average Score 332.10 (for 110 correct submissions)
The basic algorithm for this problem is relatively straightforward. The basic idea is to merge entries in the thesaurus until no more entries can be merged:
bool merged = true
while(merged){
merged = false
for each pair of entries (i,j){
if(entries i and j share 2 or more words){
merge entries i and j
merge = true
}
}
}
The details of the implementation, however, leave a lot of room for variation.
There are a number of different ways to represent the entries. You can use
arrays of strings, or more complicated data structures. If you use your
language's built in set data structure, you can use the intersection method and
the union method, which make it easy to determine if two entries share 2 or more
elements, and also easy to merge two entries. Using arrays to represent the
entries is probably a bit more work, but its not too hard to code.In the end, you need to sort words in the entries, and then sort the entries, but this is just standard sorting, with no bells or whistles. Diving

Used as: Division One - Level One:
Value 250 Submission Rate 162 / 169 (95.86%) Success Rate 118 / 162 (72.84%) High Score gladius for 233.67 points (7 mins 36 secs) Average Score 175.96 (for 118 correct submissions)
First, you should parse the input by finding the 4 ratings that are known.
While you can use floating point numbers, you have to be careful, and its safer
to just stick with integers so that you end up storing the 4 ratings as integral
numbers of 10ths. For example, you parse 4.5 as 45 10ths.
Similarly, you store the degree of difficulty and the needed score as integral
values. By storing the degree of difficulty and ratings in 10ths,
and needed in 100ths, the multiplication works out the same so that
multiplying the ratings by the degree of difficulty can be directly compared to
needed.
Once you have the input parsed, you can either iterate through all possible
ratings for the "?.?", and find the smallest one that works, or you work out the
different cases. Assuming you don't iterate, there are three different cases:
- ?.? is the lowest rating
- ?.? is a middle rating
- ?.? is the highest rating
If ?.? is a middle rating, then we discard the highest and lowest given ratings and find the sum of the remaining two given ratings, sum. So, the final score is degree of difficulty * (sum + x) where x is the value of the ?.?. Since this has to be greater than or equal to need, we have:
degree of difficulty * (sum + x) >= need ->
x >= (need - degree of difficulty*sum)/(degree of difficulty)
So, we pick the smallest valid x that satisfies this inequality, and make sure that it is not greater than the largest given rating (which was discarded).
Finally, there is the case where the ?.? is the highest score. In this case, the final score is the sum of the 3 highest given ratings times the degree of difficulty. If this is high enough, then return the value of the highest given rating.
If none of these three cases works, return "-1.0". ShortCut

Used as: Division One - Level Three:
Value 1100 Submission Rate 6 / 169 (3.55%) Success Rate 0 / 6 (0.00%) High Score null for null points (NONE) Average Score No correct submissions
Clearly, there is no way to evaluate all possible offroad paths, so we need to figure out what sort of cases warrant going offroad. First off, let's look at the general case where we start at some point on one road, and travel offroad to some part of another road, and then travel to the endpoint of the destination road. Assume that our origin point is fixed, and we want to figure out the optimal point to head for on the destination road. Also, assume that the optimal point is somewhere in the middle of the destination road, not one of its endpoints.
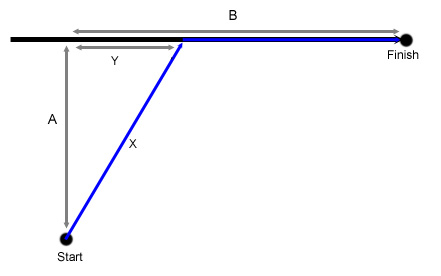
In this case, the time required to travel from the start to finish is:
2*X + B - Y = 2*sqrt(A*A+Y*Y)+B-Y
Since we want to minimize this value, we can take the derivative of this
formula with respect to Y, and want the derivative to be equal to 0 (to find the
min):
2*Y/sqrt(A*A+Y*Y)-1 = 0
2*Y = sqrt(A*A+Y*Y)
4*Y*Y = A*A + Y*Y
3*Y*Y = A*A
Y = A/sqrt(3)
Perhaps it intuitively obvious, but this confirms the value of B is insignificant, so long as it is large
enough. Therefore, it doesn't matter whether we are going all the way to the
endpoint of the road or not, we should always head to the same place along the
road. Now we know where to head to on a destination road, but we don't know
which starting points we have to consider. It might seem like we must consider
cases where we start on the middle of one road, and go to the middle of another
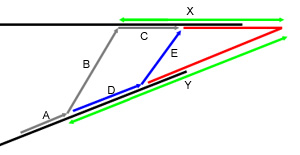
road. However, it turns out that this case will never be optimal. Imagine that
we take the gray path in the figure. This path has length A+2B+C.
The blue path, on the other hand, has a length of 2E+D+A.
Let's assume that the gray path is shorter than the blue path.
By similar triangles, we know that there is some fraction p < 1 such
that B*p = E, X*p = X-C, and Y*p = Y-D.
Assuming the grey path is shorter than the path
along D and E, we know that 2*B+C < 2*E+D and therefore, by
substitution:
2*B+X-X*p < 2*B*p+Y-Y*p.
This implies that
2*B+X-Y < p*(2*B+X-Y), and therefore, since 2*B+X-Y > 1,
we have 1>p, which is a contradiction. By similar reasoning, we can
work out the case where the roads are heading away from each other (they are
heading towards each other in the figure), and find that we should never travel
from midpoint to midpoint in that case either.
Therefore, we find that an optimal path need never travel from the midpoint of
one road to the midpoint of another road. Each offroad leg of the trip will either
start or end at an endpoint of one of the roads. Once you come to that
conclusion, there are a number of ways to proceed. One way is to find all of
the important points along the roads. A point is important if it is an
endpoint, of if it is a point in the middle of a road such as that in the first
figure (noting that start and finish can be swapped in the figure, and the case
is essentially the same). Once you find all of the important points, you can run
any standard graph algorithm. However, finding all of the important points is a
bit tricky with all the geometry, so I elected to take an approach that required
less geometry.
For the case shown in the first figure, I ran a search along the horizontal road
segment to find the best point to visit. This approach used a standard search
method to find a local minima and required no more geometry than finding the
distance between two points. With this approach, I considered the following 4
different cases for non adjacent points (black lines are roads, blue lines are
paths) between each pair of points in the input, and then ran Floyd-Warshall's
algorithm to find the minimum length path. You could also use the search
approach to find all of the important points as described previously, but there
could be a lot of important points, and you'd have to use a graph algorithm
other than Floyd's.