Introduction

I started writing this as an article about series and recurrence relations, but linear recurrences kept coming up in all the examples I used, so I decided to focus on them explicitly. A linear recurrence is a sequence of vectors defined by the equation x_i+1 = Mx_i, for some constant matrix M.

Why is this such a useful model? Let's look at some problems that can be put into this form:

Fibonacci sequence

Let

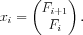
Then

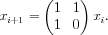
This approach works for any sequence whose ith term is defined as a linear combination of the preceding k terms.

Randomised state machines

Imagine a state machine with N states. For each state, there is a probability distribution describing the state in the next time step. If x_i is the probability distribution of states after i time steps, then x_i+1 = Mx_i where M contains all the transition probabilities. This type of model is known as a Markov model and is often used in statistics.

Evaluating series

Like the Fibonacci sequence, many series can be calculated from this form. For example, let a_i = 1+2c+3c²++ic^i-1, for some constant c, and let

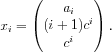
Then

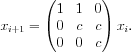
Path counts

Given a directed (or undirected) graph, let P_i be a matrix such that element j,k is the number of paths of length i that start at j and end at k (possibly visiting vertices multiple times). Trivially, P₀ is the identity and P₁ is the adjacency matrix. It is possible to show that P_n = P₁nP₀.

Fast exponentiation

Let's step back for a moment and review a technique that is probably well-known to many TopCoders: computing a^b quickly when b is large. The brute-force approach takes O(b) time, but using a recursive divide-and-conquer algorithm takes only O(log b) time:

• If b = 0, then the answer is 1.
• If b = 2k is even, then a^b = (a^k)².
• If b is odd, then a^b = a ⋅ a^b-1.

The same technique works for raising a square matrix to an arbitrary power, simply replacing 1 with I, the identity matrix. A handy trick for C++ competitors in TopCoder is to write a matrix class with an overloaded multiplication operator and a constructor that takes an int, and to use GCC's non-standard __gnu_cxx::power function (defined in ext/numeric). For a brute-force matrix multiplication, this will take O(n³ log b) time for an n × n matrix (asymtotically faster matrix multiplication is possible, but not worth the effect to implement in a TC match).

This is all that is necessary to evaluate a linear recurrence quickly. Simply note that applying the recurrence n times gives x_n = Mⁿx₀, evaluate Mⁿ as described, and multiply the result with x₀ to get x_n.

A common idiom in TC and other challenges is to ask for an answer modulo some number p, since the actual answer is too large to easily represent. This technique works just as well for these situations, because the only operations that are performed are addition and multiplication. For each basic computation, take the result modulo p. You must, however, be more careful than usual about overflow, because even if M contains small entries, the fast exponentiation algorithm may multiply together two matrices with large entries. You should ensure that p² is not too large for the type you are using.

Closed-form formulae

This algorithm is fast enough for almost all practical applications, but there are situations in which it is useful to have a formula for the ith term of a sequence. At this point, the mathematics gets a little heavy, and if your eyes start to glaze over, you should skip ahead to the example. A powerful tool in analysing matrix computations is the Jordan canonical form. Every square matrix M with real or complex entries can be written in the form M = P-¹JP, where J has a special form. It has special types of block matrices along the diagonal and zeros everywhere else:

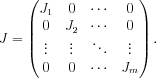
Each block matrix J_i has a constant value down the diagonal, 1's immediately below the diagonal, and zeros everywhere else. The values on the main diagonal of J are the eigenvalues of M. For almost all matrices M (technically, a set whose inverse has measure zero), each block matrix J_i will be 1 × 1, and J will simply be a diagonal matrix. Raising a diagonal matrix to the power of n is trivial (just raise each element to n), and this makes it straightforward to compute Cⁿ = P^-1JⁿP.

For some matrices, there are 1's below the diagonal in J. This makes it more difficult to compute Jⁿ, but it can still be done with a closed formula, and so a formula for Cⁿ still exists. The terms of the formula for Cⁿx₀ all have the form n^kλⁿ, where k is some constant and λ is one of the eigenvalues. Furthermore, if λ has multiplicity m, then k cannot exceed m - 1. Although the coefficients can be found by direct calculation, it is easier to solve for them by examining the initial terms in the sequence.

Let's do a practical example: the Fibonacci sequence. We saw above that the corresponding matrix is

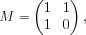
which has a characteristic equation of t² - t - 1 = 0. A useful result for Fibonacci-like sequences is that the characteristic equation for a recurrence a_i = c₁a_i-1 + + c_ka_i-k is t^k = c₁t^k-1 + + c_k. In this case, the roots are φ and 1 - φ (φ = 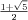being the Golden Ratio). There are no repeated eigenvalues, so the general form of the solution is F_n = pφⁿ + q(1 - φ)ⁿ. We also know that F₁ = F₂ = 1, and solving for p and q simultaneously gives p = 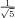and q = -.

As another example, let's look at the arithmetic-geometric progression listed in the introduction. In this case, the matrix M is upper triangular and so the eigenvalues are on the diagonal: 1, c and c. For now, let's assume 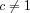, so 1 has multiplicity 1 and c has multiplicity 2. The general form is thus pncⁿ + qcⁿ + r. The first three terms are a₁ = 1,a₂ = 1 + 2c,a₃ = 1 + 2c + 3c². Provided that 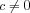, solving for p, q and r simultaneously gives p = 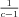, q = - 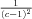and r = .

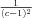In programming challenges, the closed-form formula is not always useful for calculation purposes. For example, the formula for the Fibonacci sequence contains 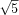in several places, which means that any calculation using floating-point values will develop inaccuracies. Raising an inaccurate number to a large power will also magnify any errors, in much the same way that compound interest magnifies your money. Even if it is possible to avoid irrational numbers, divisions complicate any algorithm that attempts to do all calculations modulo p.

The closed-form formulae are, however, useful for algorithm analysis. For example, a recursive function f(i) that calls both f(i - 1) and f(i - 2) will have running time proportional to the Fibonacci sequence, and it will be useful to know how fast this sequence grows. Thanks to the closed formula, we know that it is O(φⁿ) (the eigenvalue(s) with largest magnitude will always dominate the expression). For a conservative estimate, it is not even necessary to compute the coefficients of the general form, although in some cases the apparently dominant term will have a coefficient of 0 and thus disappear.

Sample problems

Division 1 of SRM 377 is the match that inspired me to write this article. Unfortunately, it was unrated (for technical reasons) and so the problems are not in the problem archive, but you can find them in the practise room.

SquaresInsideLattice

The required number is the sum of a series. The sum is small enough to evaluate in a loop, but for practice, try to find the closed formula. Hint: for a polynomial P, the series P(0) + P(1) + + P(n) is always a polynomial of one degree higher, for which you need only find the coefficients.

GameOnAGraph

The white moves can be represented by a matrix W and the black moves by another matrix B. If the number of moves is even, then the matrix describing the entire game is (BW)^n∕2.

AlienLanguage

If the empty string was legal, the number of words would be the product of the number of vowel-only words and the number of consonant-only words. Prove that each of these is an arithmetic-geometric progression and evaluate it.

Other problems that you can look at:

FibonacciSequence

A very simple problem based on the Fibonacci sequence. You won't need any of these techniques, but you can use it as practise.

TourCounting

This is the path counting problem mentioned in the introduction.

TurtleGraphics

Each of the basic operations can be encoded in a 4 × 4 matrix, where the top-left 3 × 3 part is a rotation matrix and the top-right 3 × 1 part is a translation.

Conclusions

Whenever you are required to evaluate a sequence x_n for some very large value of n(too large for an O(n) algorithm), it may be worth trying to express the problem as a linear recurrence, even if it is apparently non-linear. Some ingenuity may be required, for example, to find a vector containing 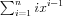which can be updated linearly. Once this has been done, however, the rest is a mechanical process.