Match Editorial

Match summary

SRM 406 proved to be rather difficult for both divisions, which had completely disjoint problem sets.

Division 1 coders made short work of the easy problem, with several coders submitting correct solutions within 3 minutes of the start of the match. However, many people were caught off-guard by a challenging medium problem and a daunting hard problem which nobody correctly solved. The challenge phase was very active, with a high number of failures on the medium problem. yuhch123 won his second SRM with the help of 150 challenge points, allowing him to pass up TCO '08 champion tomek, whose hard problem failed the system tests. Rounding out the top 3 was ploh, who had the most points gained from raw problem submissions.

Division 2 had a problem set that was harder than average at just about every problem level. The easy problem was rather straitforward, but required a bit more coding than usual and thus was easy to make a small mistake on. The medium problem required a few math tricks to solve properly, while nobody solved the challenging hard problem, which was perhaps a bit harder than a normal division 1 medium problem. In the end, sunny87 won the division with 25 challenge points and fast submissions on the easy and medium, while Rasifiel and maksay both advanced to division 1 and rounded out the top 3 spots.

The Problems

Value	250
Submission Rate	452 / 589 (76.74%)
Success Rate	357 / 452 (78.98%)
High Score	peterLiang for 235.75 points (7 mins 4 secs)
Average Score	162.17 (for 357 correct submissions)

We can solve this problem by simply iterating through each empty cell and checking to see if it is 1-happy, 2-happy, or 3-happy (or none). One way to check to see if a cell is x-happy is to manually check each possible orthogonal neighbor of the cell to see if they are all occupied, then check to see if all of the diagonal neighbors are occupied. However, this approach is very cumbersome and error-prone, and there is indeed a simpler way to perform our check.

Notice that each neighbor of a cell at coordinates (x,y) are at coordinates (x+dx,y+dy), where dx and dy are between -1 and 1 (however we can't have them both be zero!). A popular trick to exploit this property is to use distance arrays. We will have distance arrays for the x and y dimensions, where the pair dx[i] and dy[i] tell us the vertical and horizontal distances to a specific neighbor of our reference cell. Here is a sample java implementation of this approach:

int[] dx={+0,+0,+1,-1,+1,+1,-1,-1};
int[] dy={+1,-1,+0,+0,+1,-1,+1,-1};
public int[] getHappy(String[] grid) {
    int n = grid.length, m = grid[0].length();
    int[] ret = {0,0,0};
    for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) if (grid[i].charAt(j) == '.') {
        boolean a = true, b = true;
        for (int k = 0; k < 8; k++) {
            int ni = i + dy[k], nj = j + dx[k];
            if (ni < 0 || nj < 0 || ni == n || nj == m || grid[ni].charAt(nj) == 'X') continue;
            if (k < 4) a = false;
            else b = false;
        }
        if (a && b) ret[0]++;
        else if (a) ret[1]++;
        else if (b) ret[2]++;
    }
    return ret;
}

Value	500
Submission Rate	265 / 589 (44.99%)
Success Rate	64 / 265 (24.15%)
High Score	chadnov for 480.20 points (5 mins 48 secs)
Average Score	320.43 (for 64 correct submissions)

The constraints on this problem are too high to simply iterate through each integer between 1 and 10^9, checking to see if each one satisfies our criteria along the way. However, a couple of observations allow us to greatly speed up this approach and arrive at a fast algorithm. First, we note that in order for an integer K to satisfy the criteria, it must be a divisor of multiples[0].

Now, assume that K is a divisor of M, and K > sqrt(M). Now let L = M / K. Now we can observe that L < sqrt(M), since we know that L * K = M, and K > sqrt(M) implies that if L >= sqrt(M), L * K would be greater than M, which would be impossible! This observation allows us to only iterate through divisors of multiples[0] that are in between 1 and sqrt(multiples[0]), because checking each such divisor D and multiples[0] / D will enumerate all divisors of multiples[0].

So now we need to iterate through at most sqrt(10^9) potential divisors of multiples[0], which is less than 500,000 (of course, the maximum number of actual divisors will be much smaller than this). So if B is a divisor of multiples[0], we can simply iterate through the rest of the multiples array to see if B is a divisor of all of them, and we can similarly check to see if B is a multiple of each element of divisors (and similarly for multiples[0] / B). You can view daniele_s's solution for a complete implementation of this approach.

Exercise: Show how we can avoid iterating through each element of multiples and divisors per number we check.

Value	1000
Submission Rate	7 / 589 (1.19%)
Success Rate	0 / 7 (0.00%)
High Score	No correct submissions
Average Score	No correct submissions

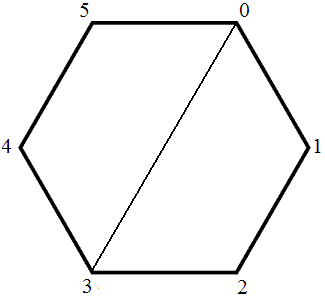
This problem was fairly tough for a division 2 hard, as evidenced by the statistics. However, if you can solve this problem conceptually, the coding stage is quite simple. Say we have a regular hexagon, and we want to start drawing diagonals. We may as well start by looking at all the diagonals that we can draw coming out of vertex 0, so let's see what happens when we draw the diagonal (0,3). It's tempting to draw this diagonal, recursively compute the number of safe sets for both sub-polygons induced by the diagonal, and multiply the result. However, this method will count the same sets many times, so it will give incorrect results.

We can take care of this problem by coming up with a unique way to seperate the polygon into sub-polygons. One way to do this is to realize that either vertex 0 will have no diagonal attached to it, or it will have a unique highest-numbered vertex attached to it by a diagonal. So we can iterate through each vertex between 2 and 4 and try it as our "leftmost" neighbor. Of course we still need a way to make sure that after we recurse on the sub-polygons induced by this diagonal, we don't draw a diagonal from a higher index back to vertex 0. We can accomplish this by recursing on the sub-polygon induced by the vertices from 3 to 5 and the diagonal (0,3) as an edge (assuming we're still trying to draw the "3" diagonal), and the sub-polygon induced by the vertices from 0 to 3 and the diagonal (0,3) as en edge. But if we aren't careful, we may try drawing the diagonal (0,3) again. We can avoid this by passing along a boolean variable telling us if we're allowed to use the first available diagonal (so after drawing diagonal (0,3) this value is false).

boolean[][] ok;
boolean[][][] got;
long[][][] dp;
final long MOD = 100000007;
int N;

public int getWays(int _N, int[] colors) {
    ///////////////////////////////////////
    N = _N;
    ok = new boolean[N][N];
    got = new boolean[N][N][2];
    dp = new long[N][N][2];
    for (int i = 0; i < N; i++) for (int j = i + 1; j < N; j++) {
        ok[i][j] = ok[j][i] = (colors[i] != colors[j]);
        if (i + 1 == j && !ok[i][j]) return 0;
    }
    if (!ok[0][N-1]) return 0;
    return (int)solve(0,N - 1,0);
}

long solve(int low, int high, int upper) {
    if (low + 1 >= high) return 1;
    if (got[low][high][upper]) return dp[low][high][upper];
    got[low][high][upper] = true;
    long ret = solve(low + 1,high,1);
    for (int i = low + 2; i < high + upper; i++) if (ok[low][i])
        ret += solve(low,i,0) * solve(i,high,1);
    ret %= MOD;
    return dp[low][high][upper] = ret;
}

Value	250
Submission Rate	399 / 415 (96.14%)
Success Rate	324 / 399 (81.20%)
High Score	Michael_Levin for 247.84 points (2 mins 39 secs)
Average Score	206.75 (for 324 correct submissions)

With an upper bound of 8 elements on the dogs array, it should be clear that a brute-force solution will suffice. Indeed, each permutation of dogs represents a way to represent the data in a pie chart, so we can enumerate each permutation of the dogs array and see which one contains the most dividing lines.

So assume we have a fixed permutation of the dogs array, and we wish to determine how many dividing lines it has. Let us create an array uncovered[], where uncovered[i] means that there is no solid region from position i in the pie chart to position i + 1 (where there are 100 positions). We can then iterate through our permutation, and for each element dogs[i] of the permutation, we can set uncovered[S] = 1, where S is the sum of all the elements of dogs iterated through so far, including dogs[i]. Then we can determine how many values of i exist such that uncovered[i] and uncovered[(i + 50) % 100] are both 1. The number of dividing lines is then this value divided by 2, since we've counted each dividing line 2 times.

To actually generate the permutations, C++ users can make use of the next_permutation function, whereas people who use other languages will have to write their own. Writing a permutation generator is a matter of simple recursion, where we just recursively determine the next element of a partial permutation repeatedly. One advantage of doing this manually for this problem is that we can keep track of the number of dividing lines as we generate the permutations, which gives us a small performance increase. Another optimization we can make exploits the symmetry of the pie chart, in that we can always assume that dogs[0] is the first element of the pie chart. An implementation of a java solution with these enhancements follows:

boolean[] ok = new boolean[51];
int[] dogs;

public int getLines(int[] _dogs) {
    dogs = _dogs.clone();
    if (dogs[0] < 50) ok[dogs[0]] = true;
    return solve(dogs[0], 1) + (dogs[0] == 50 ? 1 : 0);
}

int solve(int sum, int mask) {
    int ret = 0;
    for (int i = 0; i < dogs.length; i++) if ((mask & (1 << i)) == 0) {
        sum += dogs[i];
        if (sum <= 50) ok[sum] = true;
        ret = Math.max(ret, (sum > 50 && ok[sum - 50] ? 1 : 0) + solve(sum, mask | (1 << i)));
        if (sum <= 50) ok[sum] = false;
        sum -= dogs[i];
    }
    return ret;
}

Value	500
Submission Rate	175 / 415 (42.17%)
Success Rate	32 / 175 (18.29%)
High Score	ploh for 365.42 points (18 mins 45 secs)
Average Score	250.77 (for 32 correct submissions)

This problem can be solved by a "smart" brute-force algorithm. Before we solve the problem though, let's consider the simpler variation where the paper is restricted by having only one row. Suppose that we want to generate all resulting pieces of paper made by a sequence of folds on a 1xN sheet of paper. We can observe that (N-1)! is a very loose upper bound on the number of possible resulting sheets of paper, since there are at most N-1 ways to perform a first fold, at most N-2 ways to perform a second fold, and so on. Thus we know that an algorithm that generates each piece of paper should be reasonably efficient. We want to apply this algorithm to find each subset of cells (columns) in the initial sheet of paper that can eventually be combined onto a single cell.

Note that each cell in the initial sheet of paper can be seen as a set that contains only itself. However, let's see what happens when we perform a fold in the center of the sheet ({0},{1},{2},{3}) (remember that we are representing each cell as a set of cells that initially contains only the cell itself!). What happens when we fold along the center of the paper? Cells 0,3 and 1,2 will overlap to create the new sheet ({0,3},{1,2}). We can now deduce that it is possible for cells 0,3 to be combined into a single cell, as well as cells 1,2. Folding again tells us that all four cells may also be combined into a single cell. Note that by enumerating all resulting sheets of paper in this manner, we also enumerate all possible sets of cells that may be combined onto a single cell. We now know each subset of cells that can be combined into a single cell, and thus we can examine them all and take the set with the largest sum of elements to completely solve our simplified problem.

How can we apply this solution to solve the more general problem at hand? First we can observe that it doesn't matter what order we perform the vertical and horizontal folds in with respect to each other. Therefore, we can try each combination of vertical folds with each combination of horizontal folds, and see which one gives us the best result. However, this approach is too slow. Note that all we actually need to know is which subsets of columns can be combined into a single column, and which subsets of rows can be combined into a single row. So by taking the solution to the simplified problem above, we can try each subset of rows and each subset of columns that we know may be combined, and sum up the values of the cells that belong to both column and row subsets, keeping track of the maximum such value. You can view rem's solution for an implementation of this approach.

Exercise: Show how to avoid computing all possible folds in the precomputation step, and instead directly compute all possible sets of "combinable" rows and columns. Hint: What can you say if you know a given set of cells can combined into one cell for a sheet of paper of length L?

Value	1000
Submission Rate	9 / 415 (2.17%)
Success Rate	0 / 9 (0.00%)
High Score	No correct submissions
Average Score	No correct submissions

Despite its intimidating statstics, this problem is actually quite approachable. The first thing we should do is gain a firm grasp on the graph's special structure. Let V=v1,v2,...,vn be the unique simple path from start to end so that v1=start, v2=end). Now assume that we have two vertices vi and vj, where j > i, along this path that are a part of the same cycle. Then we can show that all the vertices between vertices i and j must be part of this cycle also.

So we can visualize our graph as a path with several simple cycles that we can take zero or more times along the way. If P is the length of the simple path from start to finish, then every path length between start and finish can be described by P + (C₁*x₁ + C₂*x₂ + ... + C_t*x_t), where the C_i's are the lengths of the cycles that we can choose to take along our simple path and x_i is a variable describing how many times we take cycle i. The problem then boils down to finding the kth smallest value of C₁*x₁ + C₂*x₂ + ... + C_t*x_t.

The case where t=1 is trivial, as we can just return k*C₁, so let's look at what happens when t=2. To simplify things further, let's try finding the kth largest value of x + y. We can reformulate this sub-problem by finding the smallest value of M such that the number of (non-negative) values x and y take on such that x + y ≤ M is at least k. This step can be accomplished via a binary search, but it would help to know what our upper bound on M is, so let's give our attention to finding the number of values that x and y may take so that x + y ≤ M for a fixed value of M. One way to do this is to iterate through all values of x, and for each value, determine how many values y may take on. With a little algebra, one can show that this is about equal to the sum of the first M integers, which is O(M^2). Therefore, we know that the largest potential value of M is O(sqrt(k)). When we expand the problem to examining cases such as C₁*x + C₂*y, the same line of reasoning can show that the largest value of M we must examine is O((C₁ + C₂)*sqrt(k)).

Of course, the above algorithm only solves a special case of the problem, but it gives us insight as to how large the return value may be, suggesting that it may be possible to search for it. Intuitively, cases with more than 2 cycles should have smaller return values than cases with only 2 cycles, because more cycles mean more ways to get the same path lengths (another way to think of this is that DP is a "good" way to solve knapsack-like problems because of the overlapping subproblem property). This idea tells us that if we have more than 2 cycles, the return value will be reasonably small, and this is the crucial observation required to finish off the problem (indeed, the largest value for a case with t > 2 has a return value of under 3 million).

The solution for finding the kth smallest value of C₁*x₁ + C₂*x₂ + ... + C_t*x_t where t > 2 is found via dynamic programming. We can use dyanmic programming to incrementally keep track of the number of ways to express every positive integer H as the sum of our cycles. We keep a running sum that tells us the total number of paths we've computed so far, and once this exceeeds k, we return the current path length. The beauty of this approach is that we don't even need to know how large our return value may be! We can use the "rolling memory" technique which takes advantage of the fact that the largest cycle length is under 500, and so we need at most the last 500 entries in our DP table at a given time. A java solution to this "reduced" problem follows:

long solve(int[] cycles, long k) {
    int n = cycles.length;
    if (n == 1) return k * cycles[0];
    else if (n == 2) return solve2(cycles[0],cycles[1],k);
    long[][] dp = new long[512][n];
    dp[0][0] = 1;
    int ret = 0;
    while (true) {
        for (int i = 1; i < n; i++) dp[ret % 501][i] += dp[ret % 501][i - 1];
        if (k < dp[ret % 501][n - 1]) return ret;
        else k -= dp[ret % 501][n - 1];
        for (int i = 0; i < n; i++) {
            dp[(ret + cycles[i]) % 501][i] += dp[ret % 501][i];
            dp[ret % 501][i] = 0;
        }
        ret++;
    }
}

long solve2(int A, int B, long k) {
    if (A < B) {
        int tmp = A;
        A = B;
        B = tmp;
    }
    int low = 0, high = 1000000000;
    while (low + 1 < high) {
        int mid = low + (high - low) / 2;
        long res = count(A,B,mid);
        if(res > k) high = mid;
        else low = mid;
    }
    return high;
}

long count(int A, int B, int bound) {
    long ret = 0;
    for (int i = 0; i * A <= bound; i++) {
        ret += (bound - A * i) / B + 1;
        if (ret > 1000000000000L) return ret;
    }
    return ret;
}