
|
Match Editorial |
Wednesday, April 23, 2008
Match summary
SRM 399 was dominated by Petr, who even without his easy submission would have won the match. Winning this match let Petr break the 3800 rating barrier, and we're all wondering how long it will be before he breaks 4000. Rounding out the top
3 spots in division 1 were tomek and bwps.
The division 1 problems were a bit harder than average, mostly due to a tricky easy problem which many people failed. Due to the tricky nature of the easy problem, the challenge phase was particularly exciting, as many submissions
were challenged within the first minute. The division 2 set was of average difficulty, and had the uncommon property that the hard problem was the same as division 1's easy problem. Division 2 was won by newcomer sange, followed by
Amir61 and OnlyK, who will all compete in division 1 for the next match.
The Problems
CircularLine

Used as: Division Two - Level One:
Value 250 Submission Rate 424 / 540 (78.52%) Success Rate 392 / 424 (92.45%) High Score ahmed_aly for 245.64 points (3 mins 48 secs) Average Score 181.45 (for 392 correct submissions)
To solve this problem, all we need to do is iterate through each pair of stations, find the fastest time to travel between them, and return the maximum of these times. Given two stations i and j where i<j, one way to go between them is just to iterate from i up to j summing up the travel time between each pair of consecutive stations. The other way is to iterate from j to n-1 (where n is the number of stations), then from 0 to i again summing up the travel time between each pair of consecutive stations. The fastest time to get from i to j (and vice-versa) is the minimum of these two values. A sample solution in C++ follows:
int CircularLine::longestTravel(vector < int > t) {
int ret = 0;
for (int i = 0; i < t.size(); i++) for (int j = i + 1; j < t.size(); j++) {
int a = 0, b = 0;
for (int k = i; k < j; k++) a += t[k];
for (int k = j; k < t.size(); k++) b += t[k];
for (int k = 0; k < i; k++) b += t[k];
ret = max(ret, min(a,b));
}
return ret;
}
Exercises:1.1: Find an O(N^2) solution to this problem.
1.2: Find an O(N * lg(N)) solution to this problem. MaximalProduct


Used as: Division Two - Level Two:
Value 500 Submission Rate 381 / 540 (70.56%) Success Rate 260 / 381 (68.24%) High Score solafide for 495.83 points (2 mins 36 secs) Average Score 397.65 (for 260 correct submissions)
While it's possible to solve this problem via dynamic programming, a simple observation leads to a much simpler solution. First, let's suppose that s is a multiple of k. Then is there any solution
better than using s/k for each ai? It turns out that the answer is no (see exercise). Intuitively, the reason this works is because numbers that are as close together as possible will give us the maximal product.
This idea can be extended to the case where s is not a multiple of k. Suppose that we start off with each number as being floor(s/k). Clearly these numbers do not
sum to s (unless s is a multiple of k). Note that the additional "sum" that's missing is s-k*floor(s/k)=s%k, which is strictly less than k. The key here is to keep our numbers as close
together as possible, so we can pick s%k of our k copies of floor(s/k) and just add 1 to them. This construction actually gives us the best possible result, as exercise asks you to prove. A sample C++ solution follows (beware of overflow!):
long long MaximalProduct::maximalProduct(int s, int k) {
int regular = s / k;
int other = s % k;
int ok = k - other;
long long ret = 1;
for (int i = 0; i < ok; i++) ret *= regular;
for (int i = 0; i < other; i++) ret *= regular + 1;
return ret;
}
Exercises:2.1: Prove that this construction works. Hint: proof by contradiction AvoidingProduct


Used as: Division Two - Level Three:
Used as: Division One - Level One:
Value 1000 Submission Rate 192 / 540 (35.56%) Success Rate 22 / 192 (11.46%) High Score sange for 729.60 points (18 mins 49 secs) Average Score 492.38 (for 22 correct submissions)
Value 250 Submission Rate 401 / 411 (97.57%) Success Rate 126 / 401 (31.42%) High Score Petr for 243.88 points (4 mins 31 secs) Average Score 181.23 (for 126 correct submissions)
While this problem wasn't terribly conceptually challenging, it was a very easy problem to make a small implementation error on. The most common bug that coders seemed to have is that they made bad assumptions
on the maximum size of numbers that could be in the result. For example, there are cases where we may need factors greater than n, and even cases where we may need factors greater than 1000.
That being said, the solution to this problem is very straitforward. One observation that helps is that we will never need a number greater than n+51 (why?). Therefore we can just iterate through all possible combinations of x, y, and z
from 1 to N+51, making sure we "break out early" if the products get too large. We must keep track of the best value of |n-x*y*z| seen so far and update if we find a better solution. We can also speed things up a bit by ensuring that x<=y<=z as we iterate.
You can view asaveljevs's submission for a nice implementation of this approach.


Used as: Division One - Level Two:
Value 500 Submission Rate 214 / 411 (52.07%) Success Rate 103 / 214 (48.13%) High Score Petr for 433.54 points (11 mins 29 secs) Average Score 274.52 (for 103 correct submissions)
While we're looking for specific permutations of the binary representations of a, b, and c, the key observation that allows us to solve this problem is that all we care about should be the number of 1's in a, b, and c. Clearly, given the number of ones
in an n-bit integer, we can deduce the number of zeros. Now let us imagine that we're looking for the least significant bit (LSB) of a', b', and c'. There are exactly 4 possibilties for these bits, because there are 2 possibilties for
the LSBs of both a' and b'. Given these bits, we can uniquely deduce what the LSB of c' must be as well. However, if the LSBs of both a' and b' are 1, then the choice for the second LSB of c' must be effected by a carry bit (just like long addition in decimal arithmetic).
We wish to build a recurrence relation based on this technique. Let us define F(a1,b1,c1,k,carry) to be the smallest result for the first (most significant) k bits of c', such that the first k bits of a', b', and c' have a1, b1, and c1 one bits, respectively.
Carry is a boolean value that tells us if the current bit must also include a carry bit from the last operation. Note that we can uniquely deduce the number of zero bits that a', b', and c' must have by computing k-a1, k-b1, and k-c1, respectively.
We can then try all possible bit combinations for the kth bit of a' and b' (which as above gives a unique value for the kth bit of c' when the carry bit is also considered). Assuming we have enough of the bits we're trying to use, we can
then recurse. For example, suppose we wish to use a '1' and a '0' as the kth a' and b' bits, and carry is 0. Then the kth bit of c' will be '1', and we examine the result of F(a1-1,b1,c1-1,k-1,0). Similarly, if we wish to use '1' and '1' as the kth a' and b'
bits and carry is 1, the kth bit of c' will be '1', and we will examine the result of F(a1-1,b1-1,c1-1,k-1,1). If this result (determined via recursion) is valid, we can then concatenate the kth c' bit and try to use this number as our final result. So we try all possible combinations of the current bits and take the minimum of all valid results.
Note that our base case is when we need to compute F(0,0,0,0,carry). Note that if carry = 1, then we have an invalid result, since we would need to add another bit to c', which we aren't allowed to do. Otherwise, the result is 0. To compute
the final answer, we simply compute F(a1,b1,c1,k,0), where a1, b1, and c1 are the number of one bits in a, b, and c, respectively. Here, k is the number of bits in a, b, and c and our carry bit should initially be set to 0. Of course we can
compute the values of F via either memoization or dynamic programming. The runtime of this algorithm is O(k^4), where k is the number of bits in a, b, and c.
As a small caveat, it may not be obvious that the above algorithm uses the "optimal substructure" property. But this can be seen because we minimize the MOST significant bits of c' at each step, and a smaller result for the most significant
bits of the result will always give us a globally optimal answer. You can view tomek's solution for an implementation of this approach.
Exercises:
4.1: Find a solution that uses O(k^3) memory and still O(k^4) time.


Used as: Division One - Level Three:
Value 1000 Submission Rate 91 / 411 (22.14%) Success Rate 23 / 91 (25.27%) High Score Petr for 896.81 points (9 mins 52 secs) Average Score 631.82 (for 23 correct submissions)
Whenever you see a problem that involves matching or pairing things together, there's a good chance that it's reducible to a maxflow problem, which is certainly the case in this problem. For readers unfamiliar with this topic, see _efer_'s tutorial.
As is the case with most flow-related problems, the challenge here is to reduce the problem to a flow problem and set up the flow network. To do so, let's suppose we want to determine if it's possible to complete exactly M rounds of dancing.
We'll set up our flow network as follows (see the figure below). The left black node will be the source and the right black node the sink. Red vertices represent boys and the grey vertices represent girls. If a boy and girl like eachother, we'll add an edge
of unit capacity between the corresponding red and grey vertices (the top and bottom edges in the figure). Otherwise, we'll add an edge of unit capacity between the blue and green nodes that are connected to the corresponding red and grey nodes (read below).
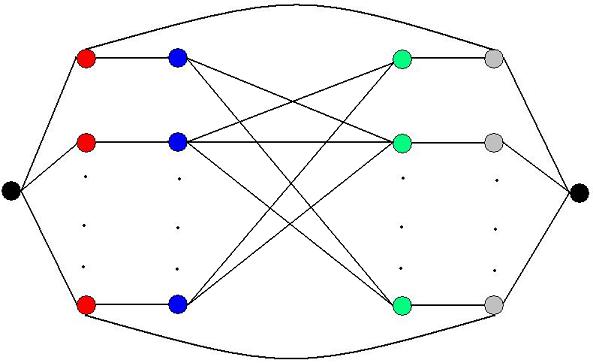
Now that we have a flow network, we will find the maximum flow between the source and the sink vertices. It can be easily shown that there can be exactly M rounds only if the flow going into the sink is equal to N*M, where N is the number of boys.
Of course, the problem remains on finding the largest M where this is true. This can easily be done by performing a binary search to find this value of M and computing a maximum flow for the network induced by each value of M we try.
However, there is a more efficient way of finding M. Suppose we know that there can be 1 round of dancing. Then we have a maximum flow in our flow network with M=1 with flow N. Now suppose we want to know if it's possible to have a second round of dancing. Then we can simply increment the capacities of the edges going out of the source and into the sink by one, and continue finding augmenting paths given the previous flow. That is, we use (or recycle) the flow for M=1 and continue finding augmenting paths to compute the maximum flow for M=2, and so on until the maximum flow is not equal to N*M. This eliminates the lg(N) factor induced by the binary search approach given above. See tomek's solution for a clean implementation of this faster approach.
Exercises:
5.1: Show how to set up the flow graph by eliminating the need for the blue and green layers.
