
|
Match Editorial |
Wednesday, November 22, 2006
Match summary
After winning the TCCC '06, Petr took his hand at writing the problems for SRM 327. Unfortunately he stumbled onto a trap that has befallen other algorithm greats before. When writing a problem set you must realize that the target audience are mortals. It would have taken a legendary coder to solve all three division 1 problems. Both the easy and medium problems were at an above average difficulty, which would leave few coders with enough time to even attempt the hard. In fact only Ying and halyavin were able to solve the 600 point problem, and only Ying was able to solve two problems. Thus most of the top scoring coders relied on the challenge phase; luckily there were many challenges for the taking, as the submission accuracy was very low. Unfortunately none of the 9 submissions to the hard problem were able to account for all the beautiful subtleties of the problem.
Division 2 was a bit more stable as several coders were able to solve all three problems, including a rather difficult medium. In the end taty was able to edge out newcomer blmarket due to the -25 points from a failed challenge.
The Problems
FunnyFence

Used as: Division Two - Level One:
Value 250 Submission Rate 451 / 499 (90.38%) Success Rate 384 / 451 (85.14%) High Score CoreDumped for 248.29 points (2 mins 21 secs) Average Score 211.67 (for 384 correct submissions)
FunnyFence is a simple problem, which asks you to find the largest fence
in a string. Coming up with an algorithm to solve the problem isn't too
difficult, but while implementing it you must pay careful attention to avoid
fencepost errors.
Typically, to avoid bugs creeping into your implementation, you should
code up the simplest algorithm you can think of that won't timeout. If you are afraid that the simple solution will timeout, you
can then make small optimizations until your algorithm is fast enough.
For example, the simple algorithm for FunnyFence is to go through every
substring and test it to see if it is a fence. To do each test you can loop
through each character in the substring and make sure that it is different
from the one right before it. This will end up looking something like:
smallest=infinity;
for(start=0 ; start<s.length ; start++)
for(end=start+1 ; end≤length ; end++)
sub = s.subString(start,end)
if( isFence(sub) )
smallest = max( smallest, sub.length)
isFence() returns true if the substring is indeed a fence. Since
there are O(n2) substrings we will call isFence() a total of
O(n2) times. Each call to isFence() could take up to O(n) time,
since it examines each character in the substring, so overall this algorithm
is O(n3). Since n is at most 50, we have plenty of time to do the
O(n3) operations.
IQTest


Used as: Division Two - Level Two:
Value 500 Submission Rate 323 / 499 (64.73%) Success Rate 47 / 323 (14.55%) High Score cax for 450.86 points (9 mins 35 secs) Average Score 320.26 (for 47 correct submissions)
IQTest would be much simpler if they gave us the values of a and
b to use -- since they didn't, it is up to our intelligence to determine
what they are.
Let's look at the simplest example first. The simplest example is example
3; there is only one value in the sequence and it is
previous0 = 0. I can think of many ways to finish this
sequence. The simplest are {0,0,0...} and {0,1,2,3...}, but there are many,
many more. In fact any sequence with only one element will have an infinite
number of ways to continue it.
Now let's look at the general case. A sequence with at least two
elements, namely previous0 and
previous1. Because of the constraint, if the sequence is
not buggy, then they must satisfy the constraint:
previous1 = a*previous0 +
b. This is one equation with two unknowns (we don't know a or
b). Since it is a linear equation, we have no hope of solving it for
both of these variables. But if we knew one of the unknowns, then we could
solve for the other ones. Well, we can't just magically know a's
value, but we can do the next best thing: loop over all possible values for
a and check for a good value.
To do this we must answer 3 questions:
- What are the possible values for a?
- How do we check if a particular value is good?
- What do we do if multiple values are good?
- It turns out that a can be at most 200 (and at least -200). The trouble is that figuring this out requires a little bit of math. Luckily you don't need to know that 200 is the bound, as long as you pick a large enough value. The first time I solved this problem I just picked 1,000,000 as my bound. I used that because it is a large value that I knew wouldn't have my program timeout. If you are unsure you can time your program with different bounds, or try to do the math to figure out the bound exactly.
- To check if a particular value of a is good you must first
calculate b. This can be done with the above equation and the first
two values of our sequence. Since we found b, now you must go through
each consecutive pair of values in the sequence and see if they satisfy the
similar constraint:
previousi = a*previousi-1 + b
If this check holds for each i, then you can use the last value in the sequence to figure out what the next value must be. - Since we are looping through every possible a you should expect that many will not pass the check. If we are lucky, only one will pass the check -- if so, we can just return the result it produces. If none pass the check, then surely there must be a BUG in the sequence given to us. Finally, what if multiple a's pass the check? You might think that this means that the sequence is AMBIGUOUS, but that isn't the case. The sequence is only ambiguous if the results produced by different a's disagree (and the only way this will happen is if the sequence is of length 2 and both elements are the same).


Used as: Division Two - Level Three:
Used as: Division One - Level One:
Value 900 Submission Rate 135 / 499 (27.05%) Success Rate 9 / 135 (6.67%) High Score blmarket for 630.68 points (20 mins 30 secs) Average Score 483.01 (for 9 correct submissions)
Value 300 Submission Rate 327 / 366 (89.34%) Success Rate 109 / 327 (33.33%) High Score abikbaev for 274.25 points (8 mins 52 secs) Average Score 185.67 (for 109 correct submissions)
Before getting into the details of the solution I want to introduce some terminology that should help:
- A string is ugly if it meets the definition in the problem statement, even if the string still has question marks within it. '?'s will count as neither vowels nor consonants.
- A string is homely if there is some way to change all of the question marks to letters in such a way that the resulting string is ugly.
- A string is nice if it is not ugly and it contains no question marks.
- A string is decent if there is some way to change all of the question marks to letters in such a way that the resulting string is nice.
Now you need to memoization functions -- one that determines if a string is homely and one that determines if it is decent. The recurrence relation just updates the state in a natural way depending upon what the character at index is. If the character is a '?' then you make two recursive calls, one if that character were to become a vowel and one if that character were to become a consonant. The base cases are if the state indicates that the string is ugly (namely, if vowels is 3 or if consonants is 5) or if you get to the end of the string and know that it is not ugly.
The dynamic programming solution is nice, but you probably had a feeling that this problem could be solved in a simpler manner. Yes, there is indeed a greedy solution which is simple to code, but as with many greedy solutions it is not so easy to prove that it works.
As with the dynamic programming solution, you will need two methods, one to determine if the string is homely and one to determine if the string is decent. In addition you should have another method that determines if the string is ugly (note that my definition of ugly explicitly tells how to treat question marks).
isUgly(): Loop over all substrings of size 3, and if any one is made entirely of vowels then the string is ugly. Similarly if any substring of length 5 is composed entirely out of consonants then the string is ugly.
isHomely(): If a string is homely then when every question mark is changed to a character, the resulting string is ugly. The string must either be ugly due to vowels or consonants. If the string is ugly due to vowels, then every character in the incriminating substring that was a question mark was turned into a vowel. Similarly if the string is ugly due to consonants, then every character in the incriminating substring that was a question mark was turned into a consonant. Thus first change all question marks into vowels. If the resulting string is ugly, then the original string is homely. Next change all the question marks into consonants. If the resulting substring is ugly then the original substring is homely. These two checks are sufficient to determine if the string is homely.
isDecent(): This method is quite a bit more complicated. Think of the string "AA?AACCCC?". The first question mark can be changed into a consonant, but not a vowel. The second question mark can be changed into a vowel but not a consonant. If there is a question mark such that changing it to a vowel makes the string ugly, then you must change that question mark to a consonant. If there is any question mark such that changing it to a consonant makes the string ugly then you must change it to a vowel. isDecent keeps looping through the string looking for such a question mark and changing any it finds until there are none left. After it changes any question mark it also does a check to make sure the resulting string isn't ugly, if so then it cannot be decent.
At some point this process must stop. The magic is that when this process does stop without having turned the string into an ugly string, the string must be decent (note that the string might still have question marks within it).
For example, look at the string: "A?BBB?A?BBB?A". None of the question marks are forced to be either a vowel or a consonant, so isDecent would not have changed any of them. How can we change the string into a nice one? Look at the leftmost question mark. Since we aren't forced to change it to a vowel or consonant, we can pick either, it doesn't matter which we choose. So lets pick consonant. Now the string is "AXBBB?A?BBB?A". Changing one question mark may result in other question marks being forced. The key is noticing that if a question mark becomes forced, then it must be the leftmost remaining question mark. Further it must be forced to be the opposite of the previous changed question mark. Changing this question mark may force another one, and so each leftmost question mark may force the one to the right of it, like dominoes falling, with each change switching between vowel and consonant. At some point we must come to the last question mark. Since at the beginning of this process each question mark could be changed either way, and each force only prevents them from one option, the changes we are making are all consistent, so the resulting string won't be ugly.
To put the solution together just make calls to isHomely() and isDecent() and if both are true then return "42". If just isHomely is true, then all resulting strings must be "UGLY" and otherwise they must all be "NICE". QuadraticEquations


Used as: Division One - Level Two:
Value 600 Submission Rate 18 / 366 (4.92%) Success Rate 2 / 18 (11.11%) High Score halyavin for 273.13 points (44 mins 26 secs) Average Score 256.03 (for 2 correct submissions)
Think of your favorite algebra teacher. She often has to create tests to
give to her students to make sure they know how to solve quadratic
equations. Wouldn't it be nice if she had a program in which she could input a solution and generate many quadratic equations with that solution? (Of course it might not be the best test if all of
the questions have the same answer). QuadraticEquations problem is much like
such a program, in fact the solution I'll present could be modified to
actually give the quadratics.
To solve this problem effectively relies on a key insight. Since you want to create the quadratic from the polynomial you must do the
opposite of what the students do when they solve a quadratic equation -- they
solve the equation by factoring the quadratic, so we must do the opposite of
factoring. Multiplication is the key.
It turns out there are two main cases, and it's easier to solve each
independently. Before I introduce the cases I'm going to make one slight
note, instead of having the solution:
(x+ y*sqrt(d) )/z
We can set y = y2 * d to reduce the number of corner cases and
have the solution:
(x + sqrt(y) )/z
Now the two cases depend on whether or not y is a perfect square.
Case 1: Y is not a perfect square
The quadratic formula tells us that a quadratic equations have two
solutions, and the difference between the solutions is the sign of the
square root of the determinant. Since Y is not a perfect square, sqrt(Y) is
not rational, so this must be the square root of the determinant. Namely the
other solution to the formula must be:
(x - sqrt(Y)) /z
Since we know both solutions, and our algebra teacher instilled in us
the knowledge that each factor must be of the form (t-solution), we now know
both factors of the quadratic. However, there might also be some other
constant factor. To find each equation we can find one equation and then
reduce the coefficients by the greatest common factor. This will give us the
smallest equation. Then we can keep on multiplying by integers until one of
the coefficients becomes too large to get the rest. The first equation we
get will just be the product of our two factors:
[t - (x + sqrt(Y)) /z] * [t + (x - sqrt(Y)) /z]
And this just so happens to come out to:
z2 t2 -2xz t + x2y
Case 2: Y is a perfect square
In this case set x= x+sqrt(y), since sqrt(y) is an integer. Thus the
solution is x/z, which is a rational number. Let p/q be this rational number
written in lowest terms with q positive. Since p/q is a root, (qt-p) is a
factor of a*t2+b*t+c. Let (ut-v) be the other factor. The problem
is we don't know what u and v are. I shall first show that u and v are
integers.
Let's let a quadratic with p/q as the solution be: a t2 + bt +
c, so we get the following equations:
at2 + bt + c = (qt-p) (ut-v) = qu t2 - (pu + qv)t +
pv
Thus a= qu, b= -(pu+qv), and c=pv.
So if we can show that a is divisible by q, then we would know that u is
an integer. Likewise if we can show that c is divisible by p then v is an
integer. Luckily we can show this by using the fact that p/q is a
solution:
a(p/q)2 + b(p/q) + c = 0
ap2/q2 + bp/q + c = 0
ap2 + bpq + cq2 = 0
If we look at this equation modulo q, then we get ap2 = 0 (mod
q). Since p and q are relatively prime this implies that a = 0 (mod q) which
is the same as saying that q divides a. Likewise, looking at the equation
modulo p, we get that p divides c. So now we know that u and v are integers,
but we still do not know their values.
As is common in such situations, if we don't know two variables we can
loop over one variable and solve for the other. To figure out which variable
to loop over we can use the above equations. Since -k ≤ a ≤ k it must
be the case that -k/q ≤ u ≤ k/q. This gives us some reasonable values
to loop over, so we will try every possible value of u. Now we must count
how many v's are possible given this particular value of u.
The constraint that -k ≤ c ≤ k means that -k ≤ pv ≤ k. So it
must be the case that abs(v) ≤ abs(k/p).
Similarly we get a constraint from -k ≤ b ≤ k. This time we get -k
≤ -pu-qv ≤ k.
That puts bounds on v such that: (-k+pu)/q ≤ v ≤ (k+pu)/q.
The two underlined equations describe all possible v's, and these are the
only constraints, so finding the intersection of these two intervals will
give you the number of solutions for a particular value of u.


Used as: Division One - Level Three:
Value 1000 Submission Rate 9 / 366 (2.46%) Success Rate 0 / 9 (0.00%) High Score null for null points (NONE) Average Score No correct submissions
This problem is quite involved. You are given a postfix expression and
asked to optimize it according to RLE-size. To do this optimization you may
make free use of associativity and commutivity. The solution to this problem
can be done in phases. The first phase is to parse the expression into a
more suitable form, namely a syntax tree. Next we must modify the syntax
tree to take into account associativity. Finally we take into account
commutivity to get the optimal size.
Step 1: Building the syntax tree
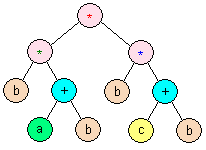
The problem statement gave a hint about how to construct the parse tree. Create a "stack calculator" program, loop through each character and, if it is a letter, create a new leaf node and push that on the stack. If it is an operator, then create a new intermediate node, pop off two nodes from the stack, and add the two nodes as children to the new node. For a well-formed postfix expression you should never have to pop from an empty stack and the stack will have exactly one node on it at the end. Note the difference between this algorithm and that for evaluating the expression: here we are placing nodes of a tree onto the stack, not the values of intermediate expressions.
Step 2: Modifying the syntax tree to account for associativity
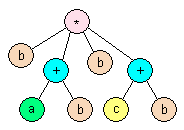
We can express this by merging the two * nodes into one node that has three children. If the operation is not commutative then we must be careful to not change the order of the sub-expressions. So we must go through the entire tree and if any operator node has a child which is the same operation, then we merge the two nodes. Doing this to the above example yields the image to the left.
Step 3: Account for commutivity and finding the optimal size
Associativity says the order of the operators doesn't make a difference. Commutativity, on the other hand, says the order of the operands doesn't make a difference. This means that we can order the four subtrees "b", "ab+", "b", and "cb+" into an order which yields the smallest overall size. To do this we are going to be somewhat greedy. I will assume that each of the subtrees has already been processed, so we know the resulting size of each subtree. Thus this algorithm is working from the bottom up through the syntax tree.
The first thing to note is that we would like to have all 3 multiplications be right next to each other in the final expression. This means that we will compute the 4 subtrees first, so that when evaluating the expression stack will have 4 values on it when it starts to do the multiplications. So in general the postfix form of a node will be: "<subtree><subtree><subtree><operator><operator>".
This means the resulting RLE size will be the sum of the sizes for the subtrees + 1. Well, almost, but not quite -- if the first character to start a subtree is also the last character to end the subtree before it, we get a savings of exactly 1. So now we must optimize the amount of savings.
The start of every subtree must be a variable (if not, then to evaluate it your first action would be to pop from an empty stack). If the root of a subtree is an operator, then the last character in the sub-expression must also be that operator. If the subtree is just a variable then it begins and end with that letter.
This allows us to put the sub-expressions into two different sets: the variables and the operations. In the example above we have 2 variables "b" and "b" and two operations "ab+" and "cb+". Now we must figure out how to order the variables and operations. One simple observation is that if you have two variables that are the same character, then you should always put them next to each other. This yields a savings of 1, which is the most you can get from any placing. Also note this doesn't prevent any future placings, since after combining the variables they have exactly the same starting and ending letters. So we can combine "b" and "b" into "bb", or equivalently we can assume there is just one "b".
We don't get a savings by putting two different variables together, because they are different characters. And we don't get any savings by putting two operations together, because they end with operators. Thus we must combine operators with variables. Yes, you guessed it; those are two disjoint sets with which we must make as many pairings as possible: Maximum Bipartite Matching.
There's one slight problem now. In order to do the matching, we must know what variables are valid starting points for the sub-expressions. Since we are doing this recursively, in a bottom up fashion, I will assume each sub-expression tells us which variables it can start, but we must figure out with which variables the entire expression can start. For example, the sub-expression "ab+" knows it can start with either a or b, and the sub-expression "cb+" knows it can start with either b or c.
For the example, we have the sub-expressions "b", "cb+" and "ab+" (I removed the other "b" because it will always be matched with the first "b"). If we match the "b" with "ab+" then we can start the entire expression with the "cb+" so c is a possible starting variable. If we match the "b" with "cb+" then we can start the entire expression with "ab+" so a is a possible starting variable. Or we can start the entire expression with the "b" that we are using to do the match. So, in general, we can start the entire expression with either any of the single variable sub-trees, or any valid starting variable of an unmatched operation sub-trees.
The tricky part is making sure the operation is unmatched. How can we verify this is the case? The simplest way is to just run the bipartite matching routine without including a particular operation. If the size of the matching obtained from this call is the same as that obtained by allowing every operation to participate, then we know that this particular operation can be left unmatched. So loop through each operation and, if you don't need to match it, then add all its valid starting variables to the list of starting variables of the entire expression.
Conclusion
This was a very nice problem that touches on many different aspects of programming. Speaking to SnapDragon in the practice room, he had this to say: "This problem has it all: a greedy algorithm you have to intuit, a tricky parsing problem, and a max flow with additional queries."
