Match Editorial

SRM 294 attracted a record-breaking 1029 participants. Boosted by 4 successful challenges, Petr scored his third Division 1 victory out of the last five matches, followed closely by bmerry and haha in second and third place. In Division 2, martin_joerg held on to first place with 3 successful challenges, followed by Multifarious in second place with 2, and jerschneid in third.

The Problems

Value	250
Submission Rate	555 / 599 (92.65%)
Success Rate	529 / 555 (95.32%)
High Score	mythruby for 249.23 points (1 mins 35 secs)
Average Score	212.48 (for 529 correct submissions)

To solve this problem, you just need to keep track of where the ace is after every swap. Use an int to store the position of the ace (0, 1, or 2), and initialize it to 1. Then, for each character in swaps, update the position. Afterward, return the appropriate letter ("L", "M", or "R") corresponding to the final position of the ace.

The following Java code implements this algorithm:

    int pos = 1;

    for (int i = 0; i < swaps.length(); i++)
        switch (swaps.charAt(i)) {
            case 'L': if (pos != 2) pos = 1-pos; break; // swap 0 and 1
            case 'E': if (pos != 1) pos = 2-pos; break; // swap 0 and 2
            case 'R': if (pos != 0) pos = 3-pos; break; // swap 1 and 2
	    case 'F':                            break; // do nothing
        }

    switch (pos) {
        case 0: return "L";
        case 1: return "M";
        case 2: return "R";
    }

Value	500
Submission Rate	292 / 599 (48.75%)
Success Rate	198 / 292 (67.81%)
High Score	mythruby for 462.34 points (8 mins 14 secs)
Average Score	268.29 (for 198 correct submissions)

Value	250
Submission Rate	389 / 430 (90.47%)
Success Rate	338 / 389 (86.89%)
High Score	oldbig for 245.36 points (3 mins 55 secs)
Average Score	177.96 (for 338 correct submissions)

This problem is similar to ThreeCardMonte, except that it more difficult to update the position of the ace. First, we'll look at how to update the position when the value of the shuffle is positive (because that case is easier), and then we'll look at how to reuse that logic to implement a negative shuffle.

Take another look at the left half of the figure from the problem statement:

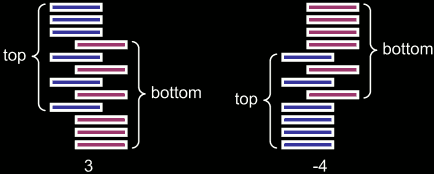
There are two cases when the position of the card doesn't change: when the ace is one of the bottom n cards, and when it is one of the top n cards. If the ace is in the bottom half of the deck, but not one of the bottom n cards, then we can update its position with the following arithmetic:

    pos = (pos-n) * 2 + n+1;

If the ace is in the top half of the deck, but not one of the top n cards, then we can update its position with the following arithmetic:

    pos = (pos - cards/2) * 2 + n;

That's all there is to updating the position of the ace for a positive shuffle. To reuse this logic to implement a negative shuffle, make use of the fact that a negative shuffle is equivalent to cutting the deck exactly in half (swapping the top and bottom halves of the deck), and then performing a positive shuffle (with the absolute value).

The Java code below implements this solution, including cutting the cards when the shuffle value is negative:

    int pos = 0;

    for (int i = 0; i < shuffles.length; i++) {

        int n = shuffles[i];

        // convert a "negative" shuffle into a "positive" shuffle
	// by swapping the two halves of the deck
        if (n < 0) {
            if (pos < cards/2)
                pos += cards/2;
            else
                pos -= cards/2;
            n = -n;
        }

        if (pos < n) {
	    // ace is in the bottom n cards
	    // its position doesn't change
	}
        else if (pos < (cards/2)) {
	    // ace is in the bottom half, above the first n cards:
	    pos = (pos-n) * 2 + n+1;
	}
        else if (pos < (cards-n)) {
	    // ace is in the top half, below the last n cards:
	    pos = (pos - cards/2) * 2 + n;
	}
	else {
	    // ace is in the top n cards
	    // its position doesn't change
	}
    }

    return pos;

Value	1000
Submission Rate	100 / 599 (16.69%)
Success Rate	6 / 100 (6.00%)
High Score	jerschneid for 733.86 points (18 mins 35 secs)
Average Score	581.57 (for 6 correct submissions)

Value	500
Submission Rate	311 / 430 (72.33%)
Success Rate	165 / 311 (53.05%)
High Score	andrewzta for 469.05 points (7 mins 23 secs)
Average Score	336.20 (for 165 correct submissions)

Palindromist was no problem for coders familiar with dynamic programming. The basic idea of dynamic programming is to pose a difficult task in terms of smaller versions of the same task. You solve the smallest tasks first, and use those results to solve the later tasks.

Here, the task is to add spaces to a sequence of letters, attempting to separate them into a list of legal words. The work you do for this task is to loop over all the words in the list, and see which ones match the beginning of the string. For each one that matches, you now have a smaller version of the same task: break the rest of the string (after the word you just matched) into a sequence of words.

If you attempt to solve this problem in a "forward" manner, starting with the complete string and using recursion to solve the smaller tasks, your solution will have an exponential running time. The reason is that there may be several different ways to arrive at the same smaller task, and your program will end up doing the same work many times. And each time it does this work, it may be solving the same even smaller task many times. A carefully crafted test case will cause such a solution to time out, and you can be certain that the system tests will include such a test case.

Using the dynamic programming approach, you solve the problem "backwards", starting with the smallest tasks. In this case that would mean starting with a single-character string, the last letter of the palindrome you are attempting to form. You store the best (smallest lexicographically) solution of each task in an array. If there is no solution, that's OK, just store some illegal value in order to record that fact. You proceed to solve larger and larger tasks (the last 2 characters, the last 3, the last 4, etc.). The key point here is that each time you match a word, you don't have to recurse on the remaining characters in the string, because you have already solved that task. You just look up the answer in the array of solutions you have been keeping.

The problem does state that you can form a palindrome in either of two ways: by repeating the last character of the input or not. This just means that you run your algorithm twice, once with each of the strings, and return the better solution.

For a clear implementation of this algorithm, see andrewzta's solution.

Value	1000
Submission Rate	57 / 430 (13.26%)
Success Rate	38 / 57 (66.67%)
High Score	haha for 842.19 points (12 mins 48 secs)
Average Score	577.74 (for 38 correct submissions)

The key to solving DigitByDigit is to realize that the optimal strategy for any state depends only on the number of blank spaces, and not on the digits that have already been placed. For example, in the states "___", "0_3_6_9", and "_55_55_", your goal is always the same: of the next three digits, try to get the highest one in the leftmost space and the lowest one in the rightmost space. The existing digits will, of course, affect the expected value, but not the optimal digit-placing strategy.

You can solve this problem by building a table of results for the solution to the problem with each number of blank spaces. For the n-digit solution, you store the expected values for each of the n digits. For example, in the 1-digit solution, the expected value of that digit is 4.5. The expected values of the digits in the 2-digit solution are 5.75 and 3.25.

Given the expected values of the n-digit solution, you can compute the expected values of the (n+1)-digit solution as follows. For each possible value of the next digit ('0' through '9'), attempt to place it in each of the n+1 positions. For each position, compute the expected value of the (n+1)-digit number, and keep track of which position yields the greatest result. Computing the expected value of the (n+1)-digit number (with one digit already placed) is easy, because you can just look up in your table the expected values of the other n-digits. Once you have determined optimal placements for each of the 10 possible digits, you can compute the expected value for each place in the (n+1)-digit number by taking the average value of that place for each of the 10 possible cases.

For example, the values 5.75 and 3.25 of the 2-digit solution can be computed by averaging the 10 values in each of the 2 columns below (because each case is equally likely to occur):

    0: 4.5 0
    1: 4.5 1
    2: 4.5 2
    3: 4.5 3
    4: 4.5 4
    5: 5 4.5
    6: 6 4.5
    7: 7 4.5
    8: 8 4.5
    9: 9 4.5

Forming a 3-digit number would lead to the following 10 cases after placing the first random digit:

    0: 5.75 3.25 0
    1: 5.75 3.25 1
    2: 5.75 3.25 2
    3: 5.75 3.25 3
    4: 5.75 4 3.25
    5: 5.75 5 3.25
    6: 6 5.75 3.25
    7: 7 5.75 3.25
    8: 8 5.75 3.25
    9: 9 5.75 3.25

The expected values for the digits of the 3-digit solution in the example above can be computed by taking the average of each column. You may notice that the values in each of the 10 cases above are always sorted from largest to smallest, and this is no accident. No optimal solution would lead to a digit having a lower expected value than one of the digits to its right. This suggests a shortcut to the algorithm above. Instead of trying each digit in each position, you can determine its position simply by finding the two values it falls between.

Once you have computed a table of solutions, all you need to do is count the number of '_' characters in the input, select the corresponding solution, and compute the expected value by multiplying the value of each digit (either given in the input or by replacing a '_' character with a value from your table) and multiplying it by the power of 10 corresponding to the position. For example, the expected value of "_55_" is:

    3.25 * 1
  + 5    * 10
  + 5    * 100
  + 5.75 * 1000