
|
Match Editorial |
Saturday, August 28, 2004
Match summary
In division 1, many coders were quick to submit the first two problems, but took their time on the hard problem. System tests then saw 13 coders solve all three problems correctly, one of them being Vigothebest, who gains 275 rating points and no longer feels blue. Eryx won the division by a comfortable margin of over 140 points, having the fastest submission time on both the medium and the hard problem. Division 2 was a close race, with algorithmus_ua winning with only 2.54 points ahead of chaochao.
The Problems
MovingAverages
Used as: Division Two - Level One:
Value 250 Submission Rate 168 / 185 (90.81%) Success Rate 161 / 168 (95.83%) High Score 35C4P3 for 243.51 points (4 mins 39 secs) Average Score 186.55 (for 161 correct submissions)
Calculating the n-moving averages for the times given proved to be no problem for the vast majority of coders. For each average to be calculated, loop through and add up the times that need to be considered for that average and do not forget to divide at the end.
C++
vector<int> calculate(vector<string> times, int n)
{
vector<int> result;
for (int i=0; i<(int)times.size()-n+1; i++)
{
int seconds = 0, h, m, s;
for (int j=i; j<i+n; j++)
{
sscanf(times[j].c_str(), "%d:%d:%d", &h, &m, &s);
seconds += 3600*h + 60*m + s;
}
result.push_back(seconds/n);
}
return result;
}
MedalTable

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 107 / 185 (57.84%) Success Rate 87 / 107 (81.31%) High Score wlott for 418.58 points (13 mins 3 secs) Average Score 292.86 (for 87 correct submissions)
Value 300 Submission Rate 170 / 175 (97.14%) Success Rate 157 / 170 (92.35%) High Score marian for 288.63 points (5 mins 41 secs) Average Score 231.45 (for 157 correct submissions)
In this problem an Olympic medals table has to be created from the results given. While this was not difficult to understand, this problem required quite some work. There were basically three steps to do: Accumulate the medals for each country, sort them by the criteria given and finally assemble the strings that are to be returned. Some coders were able to show off their language proficiency. Snapdragon for example makes nice use of vector<pair<vector<int>,string> > in his short C++ solution that can be found in the practice room.
Java
class SortEntry implements Comparable
{
int[] medal = new int[]{0, 0, 0};
String country;
SortEntry(String c)
{
country = c;
}
public int compareTo(Object o)
{
SortEntry e = (SortEntry)o;
for (int i=0; i<3; i++)
if (medal[i] != e.medal[i])
return e.medal[i] - medal[i];
return country.compareTo(e.country);
}
}
public String[] generate(String[] results)
{
Map m = new TreeMap();
for (int i=0; i<results.length; i++)
{
String[] s = results[i].split(" ");
for (int j=0; j<3; j++)
{
SortEntry entry;
if (m.containsKey(s[j]))
entry = (SortEntry)m.get(s[j]);
else
entry = new SortEntry(s[j]);
entry.medal[j]++;
m.put(s[j], entry);
}
}
SortEntry[] se = (SortEntry[]) m.values().toArray(new SortEntry[0]);
Arrays.sort(se);
String[] res = new String[se.length];
for (int i=0; i<se.length; i++)
res[i] = se[i].country + " " + se[i].medal[0] + " "
+ se[i].medal[1] + " " + se[i].medal[2];
return res;
}
LoadBalancing

Used as: Division Two - Level Three:
Value 900 Submission Rate 59 / 185 (31.89%) Success Rate 15 / 59 (25.42%) High Score Crystal for 741.23 points (13 mins 46 secs) Average Score 624.06 (for 15 correct submissions)
To achieve the fastest running time, the input chunks have to be
distributed between the two CPUs as evenly as possible. The first
thing to be noticed is that the input sizes may be divided
by 1024 to be able to work with smaller numbers. Then it is just a
standard problem (knapsack) of dynamic programming, where you loop through the
chunks and keep track of the sizes that can be achieved with the
chunks used so far. You may want to take a look at vorthys' feature
on dynamic programming for an in-depth explanation.
A lot of coders failed because they tried a greedy algorithm that
looped through the chunks (perhaps sorted) and assigned
the current one to CPU that currently has fewer work to do.
You can convince yourself with the example {3, 3, 7, 3, 1} that
this approach is doomed to fail.
C++
int minTime(vector<int> chunkSizes)
{
vector<int> dp(204801, 0);
dp[0] = 1;
int total = 0;
for (int i=0; i<(int)chunkSizes.size(); i++)
{
total += chunkSizes[i]/1024;
for (int j=204800; j>=0; j--)
if (dp[j] == 1)
dp[j+chunkSizes[i]/1024] = 1;
}
for (int i=(total+1)/2; true; i++)
if (dp[i] == 1)
return 1024 * i;
}
TopCan

Used as: Division One - Level Two:
Value 500 Submission Rate 160 / 175 (91.43%) Success Rate 146 / 160 (91.25%) High Score Eryx for 496.66 points (2 mins 20 secs) Average Score 397.36 (for 146 correct submissions)
This is an optimization problem that can be solved by differential calculus.
Apparently TopCoders know their math better than the problem writer expected
since most of them were able to solve this problem rather quickly.
These are the formulas given. V is the volume, S the surface area, h the height
and r the radius.
(I) V = h * PI * r^2 (II) S = 2 * PI * r * (r + h)Solve (I) for h and substitute h in (II).
(III) h = V / (PI * r^2) (IV) S(r) = 2 * PI * r^2 + 2 * V / rTake the derivative of S(r) with respect to r.
(V) S'(r) = 4 * PI * r - 2 * V / r^2 (VI) S''(r) = 4 * PI + 4 * V / r^3Set S'(r) = 0 to find the extremal value and assure yourself that this is indeed a minimum by stating that S''(r) > 0 for all r > 0.
(VII) 0 = 4 * PI * r - 2 * V / r^2
<=> 4 * PI * r = 2 * V / r^2
<=> 4 * PI * r^3 = 2 * V
<=> r^3 = V / (2 * PI)
(VIII) <=> r = cuberoot(V / (2 * PI))
So we can calculate r with the help of (VIII), then h with (III) and finally the minimal surface area with (II).
That is the solution most coders developed. Others like snewman performed a search to find the minimum surface area.
Java
public double minSurface(int volume)
{
double r = Math.pow(volume / (2 * Math.PI), 1.0/3.0);
double h = volume / (Math.PI * r * r);
return = 2 * Math.PI * r * (r + h);
}
CaseysArt

Used as: Division One - Level Three:
Value 1000 Submission Rate 30 / 175 (17.14%) Success Rate 14 / 30 (46.67%) High Score Eryx for 752.03 points (17 mins 34 secs) Average Score 520.93 (for 14 correct submissions)
This problem asked for the number of tilings of a rectangle by
the right tromino. It can be solved using dynamic programming
in O(length * width * 2^width).
A possible solution works as follows.
Let dp[length][width+1][2^(width+1)] be a array which holds
the number of tilings for a certain state.
Start with every element of dp set to 0.0, except
dp[0][0][0] = 1.
Loop through the rows from
0 to length-1 and in each row through the columns from
0 to width-1.
When a certain state (i,j,bitmask) is considered, a right tromino
is placed in all possible ways while occupying field (i,j)
and the number of ways to achieve the new state is updated.
A state (i,j,bitmask) whose number of tilings is stored in
dp[i][j][bitmask]
refers to a position at row i and column j in the rectangle.
Rows 0 to i-1 are completely filled and row i is
filled up to column j-1.
Bits 0 to width of bitmask are used.
Bits 0 to j of bitmask indicate
if the fields from (i+1,0) to (i+1,j) are
filled (that is in the next row) and bits j+1 to width
indicate if the fields from (i,j) to (i,width-1) are
filled (that is in the current row).
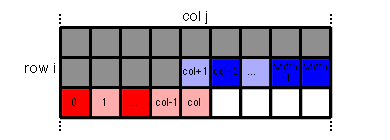
Image showing state (i,j,1101000101).
The red and blue fields are the ones whose information is stored in the bitmask.
The trominos that can be placed in this state have to cover (i,j)
and two free fields. The free fields are the ones that are light red,
light blue or white.
In order to stay within the memory limit, the array
dp[width+1][2^(width+1)] is reused for every row in the following
implementation.
C++
double howMany(int length, int width)
{
vector<vector<double> > dp(width+1, vector<double>(1<<(width+1), 0));
dp[0][0] = 1;
for (int row=0; row<length; row++)
{
for (int col=0; col<width; col++)
{
for (int mask=0; mask<(int)dp[col].size(); mask++)
{
int j0 = 1 << (col-1); // previous position in current row
int j1 = 1 << col; // position in current row
int j2 = 1 << (col+1); // next position in current row
int nxt = mask & (j2-1); // only bits set in next row
int cur = (mask ^ nxt) >> 1; // only bits set in current row
// bits 0 to i of mask hold bits 0 to i of next row
// bits i+1 to width of mask hold bits i to width-1 of current row
if (cur & j1) // (row,col) already filled?
{
// move value one column forward
dp[col+1][nxt | (cur^j1)<<1] += dp[col][mask];
}
else // place trominos
{
int newcur = cur << 1;
if (col+1 < width && (cur & j2) == 0) // (row,col+1) free?
{
if ((j1 & nxt) == 0) // (row+1,col) free?
{
// Xx
// x
int newnxt = nxt | j1;
dp[col+2][newnxt|newcur] += dp[col][mask];
}
// (row+1,col+1) is free
// Xx
// x
int newnxt = nxt | j2;
dp[col+2][newnxt|newcur] += dp[col][mask];
}
if ((j1 & nxt) == 0)
{
if (col > 0 && !(j0 & nxt)) // (row+1,col-1) free?
{
// X
// xx
int newnxt = nxt | j1 | j0;
dp[col+1][newnxt|newcur] += dp[col][mask];
}
if (col+1 < width)
{
// (row+1,col+1) is free
// X
// xx
int newnxt = nxt | j1 | j2;
dp[col+1][newnxt|newcur] += dp[col][mask];
}
}
}
}
}
// values of completed row are the values at the
// start of the next row
for (int i=0; i<((int)dp[0].size()>>1); i++)
dp[0][i<<1] = dp[width][i];
for (int i=1; i<=width; i++)
for (int j=0; j<(int)dp[i].size(); j++)
dp[i][j] = 0; // empty the rest
}
return dp[0][0];
}
See Yarin's SRM solution for an implementation of a similar approach
while using memoization.
