Match Editorial

The dragon roars again! On a Saturday when his chief rival was away, SnapDragon came from behind to take the round and, as his reward for weeks of consistent coding excellence, to recapture the number-one ranking from tomek. Will he be king of the hill for long? We look forward to an exciting tussle, preferably with more head-to-head action, in the weeks and months to come. In other news, jms137 came back with a vengeance from his premature Collegiate Challenge exit to place a strong second. Eryx continued his steady rise toward the top ten with a third-place finish.

Division Two was once again a house of pain as no one solved the Level Three, but a little birdie told me that there will now be a concerted effort to crack down on the killer problems. Patience, young coders, patience. It was a lucky thirteenth showing for riq2, who came in first by a slim three-point margin over kiveol. Not far back in third was the stalwart darkphantom, who's been gradually improving over two years with TopCoder.

The Problems

Value	250
Submission Rate	183 / 195 (93.85%)
Success Rate	167 / 183 (91.26%)
High Score	cvip11 for 244.24 points (4 mins 22 secs)
Average Score	201.83 (for 167 correct submissions)

Given the par values of an 18-hole golf course and the score obtained on each hole, expressed in relative terms such as "bogey" and "birdie", we are to compute the total score achieved by a player. There is one scoring phrase that is not relative, namely "hole in one". Coding a successful solution depends partly on dealing with this special case.

The other challenge is to find a way of translating the scoring phrases into their numerical values. The simplest approach is to use if statements or a switch to check each case individually. If we see that the phrase is "albatross", for instance, we know that it means -3 in relation to par, so we can add the par value less three to the total score. This calls for much typing, however, and the more we type, the greater the latitude for error.

Consider, instead, that we can look up the scoring phrase in an array and use its position to directly calculate a numerical value. In this array, the scoring phrases should be listed in order, say from lowest to highest as below. We then initialize the total score to zero. When iterating over the holes, we single out the "hole in one" case and immediately increment the score by one.

  public int tally(int[] parValues, String[] scoreSheet) {
    String[] scores = {"triple bogey", "double bogey", "bogey",
                       "par", "birdie", "eagle", "albatross"};
    int tot = 0;
    for (int i = 0, j; i <18; i++) {
      if (scoreSheet[i].equals("hole in one")) {
        tot++;
        continue;
      }

There are predefined functions in most languages to quickly find an element in a sorted array, but a for loop will suffice here. The scoring phrase "triple bogey" is at position 0, and its value is +3. The scoring phrase "par" is at position 3 with a value of 0. In general, we can subtract the position of a phrase and add three to obtain its value.

      for (j = 0; j <7; j++)
        if (scoreSheet[i].equals(scores[j]))
          break;
      tot += parValues[i]-j+3;
    }
    return tot;
  }

If the scoring phrases were not mapped in arithmetic progression to their values, we would probably want to use an associative array of some kind, such as a map or a hash, to look up the integer corresponding to each string.

Value	500
Submission Rate	147 / 195 (75.38%)
Success Rate	92 / 147 (62.59%)
High Score	koder for 453.07 points (9 mins 20 secs)
Average Score	324.80 (for 92 correct submissions)

Value	250
Submission Rate	163 / 165 (98.79%)
Success Rate	126 / 163 (77.30%)
High Score	antimatter for 247.25 points (3 mins 0 secs)
Average Score	211.69 (for 126 correct submissions)

We are to implement a simplified version of the word-processing feature that, given a piece of text, redistributes the line breaks so as to make every line fit tightly within a desired column width. Line breaks are not represented as such in this problem, since each line is given as a separate element of an input array.

It seems that the first task at hand is to split the lines into tokens, for which different programming languages offer various facilities. One might use Java's trusty old StringTokenizer, for instance, or resort to an even more ancient tool that comes with C++, the outrageous strtok function. An approach that translates well into any language is to do the tokenizing on the fly.

When working with Java strings at the character level, it is advisable to use StringBuffer rather than the String class, since the latter makes a whole new copy of the string with each concatenation. This makes it a painfully slow operation. Even for problems that use relatively small data sets, indiscriminate use of String concatenation can cause your program to run out of time. Beware!

In the code below, after declaring StringBuffers to store the current token and line, we initialize three integers that will serve to keep track of the token length, line index, and character index.

  public String[] justify(String[] lines, int columnWidth) {
    Vector v = new Vector();
    StringBuffer tok = new StringBuffer(), line = new StringBuffer();
    int tlen = 0, li = 0, ci = 0;

Let us consider the current character in the current line. If it is not a space, we can add it to the current token.

    while (li <lines.length) {
      char c = lines[li].charAt(ci);
      if (c != ' ')
        tok.append(c);

If the character is either a space or the last character in the current line, we have just completed a token. If the current line cannot accommodate its length, we must store it and make a fresh line that starts with this latest token. Otherwise, we add it to the current line.

      if (c == ' ' || ci == lines[li].length()-1) {
        if (line.length() >0 && line.length()+1+tok.length() >columnWidth) {
          v.add(line);
          line = tok;
        }
        else {
          if (line.length() >0)
            line.append(' ');
          line.append(tok);
        }

Furthermore, we must initialize a new token. If we have reached the end of a line, we increment the line counter and reset the character counter. Whether or not we have completed a token, the character counter must be initialized.

        tok = new StringBuffer();
        if (ci == lines[li].length()-1) {
          li++;
          ci = 0;
          continue;
        }
      }
      ci++;
    }

Once we have processed all characters, let's not forget to store the current line! Then a quick conversion from StringBuffer to String, and we're done.

    v.add(line);
    String[] ret = new String[v.size()];
    for (int i = 0; i <v.size(); i++)
      ret[i] = ((StringBuffer) v.elementAt(i)).toString();
    return ret;
  }

In typesetting systems that generate printer-ready copy, justification means not only that words are redistributed among lines, but that the spacing within and between words is adjusted so as to present a pleasing uniformity of line length. It is rumored that radeye has plenty to say on this subject if you only ask.

Value	1000
Submission Rate	12 / 195 (6.15%)
Success Rate	0 / 12 (0.00%)
High Score	null for null points (NONE)
Average Score	No correct submissions

We are asked to compute the minimum cost for a lumberjack to reach the left or right edge of a grid where cells filled with a log are always accessible, but no more than a single water cell may be traversed in the course of the trip. A problem that asks for shortest paths in a grid suggests the floodfill algorithm, which is just breadth-first search carried out in a rectangular array.

To implement floodfill, we begin by allocating an array that will store, for each cell in the grid, the minimum cost to reach it. The twist in this problem is that a two-dimensional array will not suffice, since the lumberjack may reach a cell with or without having traversed a water cell, and a minimum cost must be stored separately for each case. This is likely what tripped up many coders' efforts during the match. To see why it won't do to merge the two cases at each cell, consider the example below.

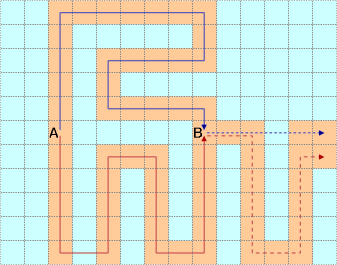
The lumberjack takes 38 seconds to travel from A to B along the solid blue line. By following the solid red line and traversing a water cell along the way, he can travel from A to B in only 31 seconds. Now if the latter route is held to be the optimal way of getting from A to B, then it seems that the lumberjack should use the dashed red line to reach safety, at a total cost of 31+19 = 50 seconds. Yet the dashed blue line, which the lumberjack can only follow if he hasn't previously used up his chance to traverse a water cell, will lead to safety at a lower total cost of 38+11 = 49 seconds.

Hence, we must take care to allocate a three-dimensional array that, for each cell in the grid, lets us store the best known cost of reaching it both with and without traversing a water cell.

  public int timeToShore(String[] riverMap) {
    int QLEN = 110000, q[][] = new int[QLEN][4], head, tail;
    int cost[][][] = new int[50][50][2];
    int dx[] = {-1, 0, 1, 0}, dy[] = {0, -1, 0, 1};
    int xx = riverMap.length, yy = riverMap[0].length(), best = -1;
    for (int i = 0; i <riverMap.length; i++)
      for (int j = 0; j <riverMap[i].length(); j++) {
        if (riverMap[i].charAt(j) == '+') {
          q[0][0] = i;
          q[0][1] = j;
        }
        cost[i][j][0] = cost[i][j][1] = -1;
      }
    q[0][2] = q[0][3] = tail = 0;
    head = 1;

We also allocate a queue that will store the grid locations we are currently exploring. You may recall from elementary algorithmics that a stack lends itself to depth-first search, which tends to be inefficient for grid exploration because it can explore rather long paths before getting around to shorter ones. Breadth-first search, which always explores shorter paths before longer ones, is implemented with a queue. In the Java code above, we declare a pair of arrays, dx and dy, that let us look up the x and y coordinate increments for each of the four directions. We also find the lumberjack's starting location and initialize the cost array with a dummy value.

    while (head != tail) {
      int x = q[tail][0], y = q[tail][1], c = q[tail][2], w = q[tail][3];
      tail = (tail+1)%QLEN;
      if (w >1 || (cost[x][y][w] != -1 && cost[x][y][w] <= c))
        continue;
      cost[x][y][w] = c;
      if ((y == 0 || y == yy-1) && (best == -1 || c <best))
        best = c;

This loop runs until the queue is empty. Here we are reading a state off the tail of the queue. Further below, we shall push new states onto its head. States that are not better than the current optimum need not be pursued any further. Otherwise, we update the optimal cost of reaching this cell in the grid, as well as the optimal cost of reaching safety, if applicable.

      for (int i = 0; i <4; i++) {
        int nx = x+dx[i], ny = y+dy[i], nc = c, nw = w;
        if (nx <0 || nx >= xx || ny <0 || ny >= yy)
          continue;
        if (riverMap[nx].charAt(ny) == '.') {
          nc += 3;
          nw++;
        }
        else
          nc += 1 + (i%2 == 0 ? 0 : 1);
        q[head][0] = nx;
        q[head][1] = ny;
        q[head][2] = nc;
        q[head][3] = nw;
        head = (head+1)%QLEN;
      }
    }
    return best;
  }

Finally, we generate a new state in each of the four directions, remembering to increment the travel cost appropriately. Notice that most of this code consists of bookkeeping for the cost grid and the state queue: initializing arrays, popping states off, pushing states on. This is routine stuff that will come to you easily once you have implemented breadth-first search a few times.

Value	500
Submission Rate	123 / 165 (74.55%)
Success Rate	75 / 123 (60.98%)
High Score	SnapDragon for 452.53 points (9 mins 24 secs)
Average Score	296.90 (for 75 correct submissions)

Given a piece of text and a mapping of plain characters to code characters, we are to overwrite with asterisks any profanity (from a fixed list of seven) that is rendered with any number of letters encoded and any number of spaces separating the letters. Formally speaking, all such renderings of a profanity constitute a regular language, which can therefore be recognized by a regular expression or, equivalently, by a finite automaton. Indeed, a few enlightened coders attempted to solve this problem by generating a state machine from the given encoding.

A less civilized approach that works just as well here, what with the limit of 50 characters in a text fragment, is to take every possible substring, of which there are no more than 50*50 = 2500, and determine by iteration whether it amounts to a profanity. First, however, to ensure that asterisks are not written over spaces adjoining a profanity, we discard substrings that begin or end with a space. For the remaining substrings, we can eliminate all spaces and think no more of them. Why should we?

  public String censor(String plain, String code, String text) {
    String[] cusses = {"heck", "gosh", "dang",
                       "shucks", "fooey", "snafu", "fubar"};
    StringBuffer clean = new StringBuffer(text);
    for (int i = 0; i <text.length(); i++)
      for (int j = i; j <text.length(); j++) {
        if (text.charAt(i) == ' ' || text.charAt(j) == ' ')
          continue;
        String sub = text.substring(i, j+1).replaceAll(" ", "");

We can easily cut down on the number of iterations by considering only those cases where the substring is exactly as long as a candidate profanity.

        for (int ix = 0; ix <cusses.length; ix++) {
          if (cusses[ix].length() != sub.length())
            continue;
          String cuss = cusses[ix];

If a character in the candidate does not equal the corresponding character of a profanity, we loop through the possible encodings to see whether one of them applies. If none of them does, we break out of the inner loop.

          int jx = 0;
          for ( ; jx <cuss.length(); jx++)
            if (sub.charAt(jx) != cuss.charAt(jx)) {
              int kx = 0;
              for ( ; kx <code.length(); kx++)
                if (sub.charAt(jx) == code.charAt(kx) &&
                  plain.charAt(kx) == cuss.charAt(jx))
                    break;
              if (kx == code.length())
                break;
          }

If we never broke out of the inner loop, then an encoding was found for every character, so we can proceed with censorship. We know the original length of the substring from the indices we used to extract it.

          if (jx == cuss.length())
            for (int k = i; k <= j; k++)
              clean.setCharAt(k, '*');
        }
      }
    return clean.toString();
  }

Censoring profanities in the real world is not nearly so simple. Quite apart from the technical difficulties involved, there is the matter of deciding what is offensive and what is not. Standards of propriety vary through time and space, but so do semantics. For instance, to tell someone that "you suck" or to say of something that "it sucks" used to mean, when the expression arose in the fifties, that the object of scorn was hollow and filled with a vacuum. It was the sort of banter that required some scientific education to appreciate fully. Today, by association with an unrelated field of endeavor, these phrases have acquired a rather more scurrilous quality.

Value	1000
Submission Rate	27 / 165 (16.36%)
Success Rate	15 / 27 (55.56%)
High Score	Eryx for 672.49 points (22 mins 14 secs)
Average Score	519.81 (for 15 correct submissions)

We are asked to calculate the steepest angle at which a hockey puck can be fired from the blue line, off the boards, and into the net while avoiding a few 50-centimeter line segments scattered on the ice. The elegant way to do this begins with the observation that unless the puck can be aimed at the right goalpost, it must graze the left endpoint of some player. For every such shot, one can verify without resorting to floating-point calculations whether the puck's path intersects any other player's line segment. Only when calculating the magnitude of the optimal angle is it necessary to compute a double value.

A less tidy approach that requires doubles throughout is to calculate the shadow projected by each player onto the goal line, keeping track of the longest intervals that are left in the clear. The right endpoint of the rightmost such interval will then supply the answer. In either approach, we can obviate the fuss of calculating rebounds by reflecting the hockey rink. The puck can then pass through the looking glass, as it were, and continue traveling in a mirror world to the right. All players are reflected indiscriminately, so that they can block the puck before or after the rebound. The straight path of travel makes it impossible for both a player and his mirror image to block the puck.

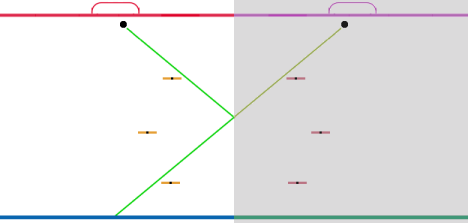
In the Java code below, we use a single loop to iterate over the players twice, using them raw the first time and reflecting them the second. Values l and r are the x coordinates that result from projecting the left and right endpoints of a player onto the goal line. We can get away with the expression iceHeight/y only because the problem constraints guarantee a non-zero y. The arrays sl and sr are used to store the left and right endpoints of the longest intervals that are not shadowed by any player so far. We shall use nsl and nsr to temporarily hold the new intervals computed in each iteration.

  public double caromAngle(int puckCoord, int[] xCoords, int[] yCoords) {
    double[] sl = new double[50], sr = new double[50];
    double[] nsl = new double[50], nsr = new double[50];
    int px = puckCoord, snum = 1, nsnum;
    px = puckCoord;
    int pnum = 2*xCoords.length;
    sl[0] = iceWidth+(iceWidth-goalWidth)/2.0;
    sr[0] = sl[0]+goalWidth;
    for (int i = 0; i <pnum; i++) {
      double x, y, l, r;
      x = xCoords[i <pnum/2 ? i : i-pnum/2];
      y = yCoords[i <pnum/2 ? i : i-pnum/2];
      if (i >= pnum/2)
        x += 2*(iceWidth-x);
      l = px + iceHeight/y * (x-playerWidth/2.0 - px);
      r = px + iceHeight/y * (x+playerWidth/2.0 - px);

We maintain the unshadowed intervals in order from left to right while calculating the effect of successive shadows. There are four types of shadow to deal with. There is a kind that obscures an interval entirely, and another that doesn't occlude it at all. Among the shadows that fall partially onto an interval, some leave an unoccluded segment to the left, and some to the right. Or perhaps both, but there is no need to deal with such cases separately.

      nsnum = 0;
      for (int j = 0; j <snum; j++) {
        if (l <= sl[j] && sr[j] <= r)
          continue;
        if (r <sl[j] || sr[j] <l) {
          nsl[nsnum] = sl[j];
          nsr[nsnum++] = sr[j];
          continue;
        }
        if (sl[j] <l) {
          nsl[nsnum] = sl[j];
          nsr[nsnum++] = l;
        }
        if (r <sr[j]) {
          nsl[nsnum] = r;
          nsr[nsnum++] = sr[j];
        }
      }
      for (int j = 0; j <nsnum; j++) {
        sl[j] = nsl[j];
        sr[j] = nsr[j];
      }
      snum = nsnum;
    }
    if (snum == 0)
      return -1;
    double x = sl[0];
    double angle = Math.atan(iceHeight/(x-px))*180.0/Math.PI;
    return angle;
  }

All our calculations use a reflected goal. Thus, in retrieving what appears to be the left endpoint of the leftmost interval, we actually obtain the right endpoint of the rightmost interval.