
|
Match Editorial |
Monday, July 28, 2003
Match summary
Winner in Division-I by a very small margin was radeye, after having successfully challenged two solutions. Because of an - again! - too hard last problem in Division-I by yours truly, everything depended on the speed on the first two problems. Fastest on these two were SnapDragon, which earned him a second place. Notably is also that tomek's streak of correct submissions ended in this SRM.
In Division-II, the medium problem caused a lot of trouble for many competitors; less than half submitted on it, and less than half of the submissions were correct. 3 people solved all three problems, and top scorer among those were lovro.
The Problems
GuessTheNumber
Used as: Division Two - Level One:
Value 250 Submission Rate 166 / 185 (89.73%) Success Rate 150 / 166 (90.36%) High Score nankinger for 249.32 points (1 mins 29 secs) Average Score 217.71 (for 150 correct submissions)
This is a pretty straightforward problem. All that has to be done is to convert the given pseudocode into legal Java/C++/C#/VB code. In C++ this can look like this:
int lower=1,guesses=0,x;
do {
x=(lower+upper)/2;
guesses++;
if (x>answer) upper=x-1;
if (x<answer) lower=x+1;
} while (x!=answer);
return guesses;
The nice thing is that finding the middle number can be done by integer division, which will give the lower middle number if there are two middle numbers, as wanted.
Salary
Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 550 Submission Rate 82 / 185 (44.32%) Success Rate 39 / 82 (47.56%) High Score lovro for 444.32 points (14 mins 35 secs) Average Score 279.20 (for 39 correct submissions)
Value 300 Submission Rate 125 / 131 (95.42%) Success Rate 94 / 125 (75.20%) High Score SnapDragon for 292.67 points (4 mins 31 secs) Average Score 200.38 (for 94 correct submissions)
The first thing to note is that all intervals are disjoint (due to the constraints), so we can treat each interval separately and then sum up the amount for each interval.
To find the amount for each interval, there are two approaches. One involves taking the difference between the departure time and arrival time for each interval and then use some if-statements to determine how much of that time was overtime. A slightly less error prone method involves simulating each second in the interval.
In both cases we should first convert the time stamp format into seconds only. To extract hour, minute and second, C++ users can use the ancient sscanf from C, like this:
sscanf(timestamp,"%d:%d:%d",&h,&m,&s); s=s+m*60+h*3600;
For the simulation approach, we loop between the two time stamps. For each second between 21600 and 64799 inclusive (that's between 06:00:00 and 17:59:59) we increase one counter, t1, for the other seconds we increase another counter, t2. For the difference approach, see radeye's solution.
The amount earned is then (t1 + 1.5*t2)*wage/3600. To avoid using doubles (which works if one makes sure to take caution when doing the rounding) this can be written as (2*t1 + 3*t2)*wage/7200. When doing this calculation, one has to use long (Java) or long long (C++) since the intermediate result with otherwise overflow. An example was included so people wouldn't make this mistake since that's not what the problem was about.
HourGlass
Used as: Division Two - Level Three:
Value 1000 Submission Rate 17 / 185 (9.19%) Success Rate 6 / 17 (35.29%) High Score Eagle13 for 505.27 points (36 mins 49 secs) Average Score 459.95 (for 6 correct submissions)
The intended solution here was brute force using recursion, basically testing all possible ways to flip the hourglasses. The prototype of the recursive function can look like this:
void go(int sand1, int sand2, int time);
The purpose of this function is to explore all possible ways to flip the hourglasses. At the beginning of the function, we mark that the current time is measurable (because this function will only be called with such time parameters). One important thing to note is that, due to the constraints, times greater than 500 will never be interesting because it can never be among the 10 shortest times. So if time is greater than 500, we can just return right away.
If sand1 or sand2 is 0, then one of the hourglasses has just run out of sand and we are allowed to flip one or both of the hourglasses. This is done by a recursive call, for instance go(glass1-sand1,sand2,time) to just flip hourglass 1. Since we are trying all possible ways to flip the hourglasses, we should try three recursive calls: flipping hourglass 1, flipping hourglass 2, and flipping both.
If there is still sand left in at least one of the hourglasses, we must also try the possibility to do nothing at the moment and let time elapse until a new event occurs (that is, when one of the hourglasses runs out of sand). If one of the hourglasses is already out of sand, this happens of course when the other hourglass runs out of sand. This case can be coded like this:
if (sand1>0 && sand2==0) go(0,0,time+sand1);If both hourglasses have sand left in them, the amount of time that has elapse before we can do anything again is minimum value of sand1 and sand2. This case can be coded like:
if (sand1>0 && sand2>0) {
int min;
if (sand1<sand2) min=sand1; else min=sand2;
go(sand1-min,sand2-min,time+min);
}
A slight problem at the moment is that the number of recursive calls will grow exponential, and the solution as it is will time out. What we have to do is to make sure we don't evaluate the function go more than once using the same set of parameters (because there's no point in evaluating the same thing again, is there?). So we need to keep a table (or a set) of the sets of parameters the function have been called with. If we ever call the function using a set of parameters which has been used before, we simply return. Otherwise we include the new set of parameters into the set. See the solution by writer in the practice room for details.
A completely different way to solve the problem is to immediately figure out what times are measurable by logic. Obviously all times in the form glass1*x + glass2*y are measurable, but also all times of the form glass1*x + z*abs(glass1*x - glass2*y). Exactly why this is so I don't know, but it works. Check out my (Yarin) short implementation of this in the practice room. This method was successfully used by mwaisdn in the SRM.
Table
Used as: Division One - Level Two:
Value 500 Submission Rate 103 / 131 (78.63%) Success Rate 92 / 103 (89.32%) High Score SnapDragon for 470.82 points (7 mins 9 secs) Average Score 334.10 (for 92 correct submissions)
This problem, which had a somewhat lengthy problem statement, is actually quite simple to implement once you understand it, since we are guaranteed that the input will be a legal table.
We can start by filling a 50x50 matrix (the maximum size of the output) with dots ('.'). Each dot will then represent a basic cell not yet filled. Now we loop through all rows in the input. Parsing the input is quite simple because each tuple is exactly 7 characters wide, so the important data is always at position 7*i+1, 7*i+3 and 7*i+5 where i is the tuple number. Thus for each element in the input, we loop through all tuples (size of string divided by 7) and extract the data.
Now, each element in the input correspond to one line in the output matrix, although some cells might extend to further lines. For each line, we find the first basic cell not used. This basic cell must then be the upper left corner of the cell described by the next tuple. Since we know that the table is valid, we just fill rowspan rows and colspan columns with the content. Once that is done, we move on to the next tuple until the line is done.
Once all this is done, we need to find out the width of the matrix (the height we already now, it's the same as the number of elements in the input), which is a trivial task now: just check where the dots begin in any of the lines. Again, since the table is valid, all lines will have the same length.
For instance, on the example in the problem statement, the procedure would be like this: (the 50x50 matrix is here shrunk to make it easier to read)
A....... ABB..... ABBC.... ABBCD... ......... ........ ........ ........ new line ABBCD... ABBCD... ABBCD... ABBCD... ABBCD... E....... EF...... EFG..... EFGH.... EFGHI... ......... ........ ........ ........ ........ new line ABBCD... ABBCD... ABBCD... EFGHI... EFGHI... EFGHI... J....... JK...... JKLLL... J....... J....... J.LLL... J....... J....... J....... ......... ........ ........ new line ABBCD... EFGHI... JKLLL... JMLLL... J....... ......... and so onPosters

Used as: Division One - Level Three:
Value 1000 Submission Rate 9 / 131 (6.87%) Success Rate 0 / 9 (0.00%) Average Score No correct submissions
So it happened again. No one solved this problem, even though there were several good attempts (and some not so good ones...). There are actually several ways to solve this problem, although one has to be careful about timeout issues in all methods.
The problem has two parts: calculating the area covered by the posters given there positions, and testing a lot of different ways to put the posters. Lets start with how to calculate the area. Since the width and height is at most 100, it's possible to have a matrix of size 100x100 and fill it with 0's and 1's and sum up the elements. This method is quite slow though, and not likely to work unless the rest of the solution is extremely optimized.
A better method is to use the inclusion/exclusion principle. Assume we have three shapes (in this problem, these are rectangles) and want to calculate the total area they cover. Call the shapes A, B and C. Let AB be the area that A and B covers in common, and define AC, BC and ABC in the same way. To calculate the total area, we can start with A+B+C. Now we have counted some areas twice, namely those that are shared by both A and B, etc. So we have to subtract AB+AC+BC from A+B+C. But then we will have subtracted by too much! Consider the area ABC - this part was included thrice in A+B+C but then removed thrice in AB+AC+BC. So we need to add ABC, and thus ends up with (A+B+C)-(AB+AC+BC)+ABC.
Does this seem familiar? It should, because this is about Venn Diagrams, something you should have learned in the school. It's not hard to generalize this to more than three shapes; in this problem we may have up to five shapes. The nice thing is that with rectangles it's very easy to calculate the common area shared by a set of rectangles: If (x1,y1)-(x2,y2) and (x3,y3)-(x4,y4) are two rectangles, the left edge of the common area is max(x1,x3), the right edge is min (x2,x4) and so on.
The whole routine to calculate the total area shared by the rectangles can be written like this: (n is the number of rectangles, xpos[i],ypos[i] is the upper left corner of rectangle i, and pw[i],ph[i] is the size of rectangle i.
int area=0;
for(int i=1;i<(1<<);i++) {
int minx=0,miny=0,maxx=wallwidth,maxy=wallheight,sign=-1;
for(int j=0;j<n;j++) {
if (!((1<<j)&i)) continue;
minx>?=xpos[j];
miny>?=ypos[j];
maxx<?=(xpos[j]+pw[j]);
maxy<?=(ypos[j]+ph[j]);
sign=-sign;
}
if (minx<maxx && miny<maxy)
area+=sign*(maxx-minx)*(maxy-miny);
}
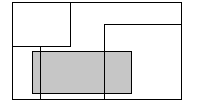 Now for the second and more interesting part. Consider an optimal
layout of the posters (ie one resulting in the maximal area of the wall
being covered). Assume we have a poster not touching any other poster
(or the wall) along it's left or right edge. It would then be possible to
move this poster left or right without decreasing the total area covered,
because if that happened, we would move it so it overlaps another poster,
and that cannot happen unless it's vertical edges first touch each other.
See the figure to the right: the gray rectangle can be moved left or right
until it's left edge touches either the wall or the right edge of the
lower left rectangle. It can then be move up or down so it's horizontal
edge also touches another edge. Thus we can always rearrange an optimal solution so all posters
touch each other (or the walls) both vertically and horizontally.
Now for the second and more interesting part. Consider an optimal
layout of the posters (ie one resulting in the maximal area of the wall
being covered). Assume we have a poster not touching any other poster
(or the wall) along it's left or right edge. It would then be possible to
move this poster left or right without decreasing the total area covered,
because if that happened, we would move it so it overlaps another poster,
and that cannot happen unless it's vertical edges first touch each other.
See the figure to the right: the gray rectangle can be moved left or right
until it's left edge touches either the wall or the right edge of the
lower left rectangle. It can then be move up or down so it's horizontal
edge also touches another edge. Thus we can always rearrange an optimal solution so all posters
touch each other (or the walls) both vertically and horizontally.
The idea now is to find an optimal solution where all posters have horizontal and vertical edges touching each other. We try place the posters in all possible permutations, always starting with putting the first poster in the upper left corner and the second poster in the lower right corner (it should be obvious than an optimal solution can always be reached by starting like this). The third poster can then be placed so it's left edge touches either the walls left edge, or the first posters right edge, or so it's right edge touches the right walls edge or the second posters left. All these possible x coordinates can be represented with an integer each - a positive integer means that the posters can be placed to the right of the x coordinate, and a negative integer means that the poster can be placed to the left of this x coordinate.
After placing the two first posters, we have four critical x points, which by this system are: 0, -width, posterWidth[0], -(width-posterWidth[1]). If we place a poster to the right of a critical point cx, we get a new critical point cx+posterwidth. If we place it to the left of a critical point cx (a negative value), the new critical point also becomes cx+posterwidth, a nice convenience. The y coordinates are of course treated the same. When deciding where to put a poster, we try all pair of critical points.
The recursive function thus becomes something like this: (pseudocode)
void go(int rectno, int[] criticalx, int[] criticaly)
{
if rectno==number_of_rectangles
calculate_area
return
end
if rectno==0
put rectangle 0 in upper left corner
go(1,criticalx+[pwidth[0]],criticaly+[pheight[0]]);
return
end
if rectno=1
put rectangle 1 in lower right corner
go(2,criticalx+[-wallwidth+pwidth[1]],criticaly+[-wallheight+pheight[1]])
return
end
loop x through all criticalx values
loop y through all critialy values
check if poster rectno can be put at x,y
if so
go(rectno+1,criticalx+[x+pwidth[rectno]],criticaly+[y+pheight[rectno]])
end
end
}
This should be enough to get it to run in time (barely). There are a few more optimziations possible though. For instance, one can skip selecting x and y from the same index in criticalx and criticaly since that will be a corner of a poster, and it's not necessary to check the case when two posters touch each other in a corner (and not along the edges). One can also speed up the solution a lot by updating the area after every placed poster. It's then possible to backtrack the recursive calls earlier, when the total area so far plus the area of the remaining posters is not greater than the best covered area found so far. Check the writer solution in the practice room for a solution where all these optimization steps have been included.
This was the complicated solution. A much easier solution is a greedy approach which surprisingly works. Again we have as outer loop to try all permutations of the posters. For each permutation we place the first two posters in the opposite corners. The third poster is then placed at the coordinates which gives the maximum area covered with the three first posters. We can simply loop over all x and y coordinates for this, and use the area formula above. Once we have decided where to put poster three, we move on to the next poster etc. Check my (Yarin) solution in the practice room for such a solution. The solution is quite slow, and barely makes it through the 8 second time limit on some cases, but can still be improved a lot. As to why it works, I've no idea. It does not work if the greedy strategy is applied to all posters (ie skipping the step of placing the first two in the opposite corners) - it gives the wrong answer on some cases then.
