
|
Match Editorial |
Wednesday, June 11, 2003
Match summary
Divison-I had a tricky medium level problem which most competitors got stuck at; in the end, only 11 people solved two or more problems. Most likely more people would have solved the hard problem if they had skipped the medium one at an early stage. Winner was (dare I say as usual?) SnapDragon ahead of bstanescu and radeye, the only three to solve all three problems. With this SnapDragon passed the 3400 rating mark, 340 points ahead of the second highest ranked - incredible! In divison-II, rustyoldman won comfortable, more than 250 points ahead of the runner-up (and first timer) skye85.
The Problems
WidgetRepairs
Used as: Division-II, Level 1:
Value 250 Submission Rate 188 / 204 (92.16%) Success Rate 150 / 188 (79.79%) High Score jimrandomh for 246.95 points
Reference implementation: rustyoldman
Implementation
We simulate each day by keeping track of the number of broken widgets the shop has each day. At the beginning of each day we check if any new broken widgets has arrived, and if so update the total count of broken widgets. If this count is greater than 0, we increase the count of how many days the repair shop has to work. We then decrease the number of broken widgets with how many the repair shop can fix in one day (just make sure the total amount of broken widgets don't go below 0, they don't create new widgets after all!).
One thing to watch out for is to know when we're done. We're done when we have no broken widgets left, and that no more broken widgets will arrive. The first condition is easy to check, and the second one is true after day 20 at the very least, since the number of elements in arrival is at most 20 (no more broken widgets arrive after day 20). The outer loop can then look like this:
while (brokenWidgets || day<=20) {
...
}
The reference solution uses a safe upper bound of 25,000 days. Check it out for a complete implementation of the problem.
InterestingDigits
Used as: Division-II, Level 2:
Used as: Division-I, Level 1:
Value 500 Submission Rate 95 / 204 (46.57%) Success Rate 76 / 95 (80.00%) High Score Spiffage for 486.51 points
Value 250 Submission Rate 119 / 123 (96.75% ) Success Rate 115 / 119 (96.64%) High Score SnapDragon for 248.83 points
Reference implementations: Yarin, SnapDragon
Implementation
We start with an outer loop from 2 to base-1, testing whether or not a digit is "interesting". If it is, we'll add it to the list of interesting values:
vector<int> digitList;
for(int i=2;i<base;i++) // Don't check 0 and 1
if (interesting(i,base))
digitList.push_back(i);
return digitList;
Now, there are two ways to check if a digit is interesting: brute force (according to the problem description) or using a discrete math property. Lets start with the brute force version.
According to the problem description, we should check all multiples of the digit, but only those having at most 3 digits. The largest number in base B with 3 digits is simply B3-1, so we have the following for-loop:
bool interesting(int d, int b) {
// Loop i through all multiples of digit, that is:
// 0, d, 2*d etc up to b^3
for(int i=0;i<b*b*b;i+=d) {
...
}
return true;
}
Now we should check that the sum of the digits of i (in base b!) is also a multiple of d. To calculate the sum of the digits, remember how we convert a decimal number to a string: we take the number modulo 10 to get the last digit, then divide by 10, take modulo 10 again to get the second last digit etc. Now, we just replace the 10 with b to make the same thing in the base we're checking:
int sum=0,n=i;
while (n) {
sum+=n%b;
n/=b;
}
if (sum%d) return false; // The digit sum is not a multiple of d!
Now to the math(emagical) solution:
bool interesting(int d, int b) {
return b%d==1;
}
Whoa! Wait a second, how can that work? Assume a digit D is interesting (that is, if A is a multiple of D, then so is the digit sum of A) in base B, and that B%D=1. Let Ai be digit i in A - that is, A = A0*B0 + A1*B1 + ... We have:
A0*B0 + A1*B1 + A2*B2 + ... ≡ 0 (mod D)
But since B ≡ 1 (mod D), we also have Bn ≡ 1 (mod D), so:
A0 + A1 + A2 + ... ≡ 0 (mod D)
And thus the digit sum of A is a multiple of D. It's slightly trickier to prove that if B%D is not 1, then D is not an interesting number, so I'll leave that as an exercise :)
BrickByBrick
Used as: Division-II, Level 3:
Value 1100 Submission Rate 12 / 204 (5.88%) Success Rate 4 / 12 (33.33%) High Score Rustyoldman for 638.90 points
Reference implementation: rustyoldman
Implementation
This problem makes you think about Arkanoid (or Break Out or whatever), doesn't it?
We should try to simulate the balls movement in the grid until all bricks are gone, or return -1 if this never happens. How can we know if this will never happen? If the ball ever appears on the same position and same direction as it has before and no brick was destroyed between these two occasions, we're stuck in an infinite loop and can safely return -1. We don't actually have to store all previous ball locations and directions, because this condition will happen if we haven't destroyed a brick in a sufficient long time. If there are only, say, 256 possible locations and 4 possible directions for the ball, if after 1025 time steps no brick has been destroyed, we must (by the pigeon hole principle) be at a location and direction we have been at before.
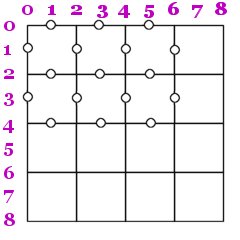 Now to the simulation. If we look at the diagram in the problem description, we see that
the relevant position of the balls is at the grid lines, not the actual squares within the grid (even though that is where the bricks are). Thus we set
out coordinate system so that x=0 means the leftmost vertical grid line, x=2 the one after that etc while the odd x coordinates indicates that the ball
is a on horizontal grid line, see figure.
Now to the simulation. If we look at the diagram in the problem description, we see that
the relevant position of the balls is at the grid lines, not the actual squares within the grid (even though that is where the bricks are). Thus we set
out coordinate system so that x=0 means the leftmost vertical grid line, x=2 the one after that etc while the odd x coordinates indicates that the ball
is a on horizontal grid line, see figure.
The ball starts at position x=1,y=0 and has direction dx=1,dy=1. During the simulation, we update the ball location (x+=dx, y+=dy) and then figure out which grid square it's adjacent too. This is slightly tricky, because you have to split into several cases: If x is even, the desired grid square is (x/2-1,y/2) if dx<0 or (x/2,y/2) if dx>0. If x is odd, then y is even (one of the coordinates is always even) and we calculate the grid square in a similar way. Once we know the grid square, we check if contains a brick or a wall (we may start the problem by adding a wall surrounding the whole grid so we don't have to check if the ball gets out of bounds). If it's a wall or a brick, the ball changes direction. If we hit a brick to the left or right (which is the case if x is even), then we change direction horizontally (dx=-dx), otherwise we change direction vertically (dy=-dy). If the square was a brick, remove it, and don't forget to reset the counter when we last hit a brick!
And that's basically it. See the reference solution for the details of how to implement all this.
StripePainter
Used as: Division-I, Level 2:
Value 500 Submission Rate 23 / 123 (18.70%) Success Rate 10 / 23 (43.48%) High Score bstanescu for 390.72 points
Reference implementations: DjinnKahn, ValD
Implementation
This was an unusually hard 500p, requiring a non-straightforward dynamic programming solution (or memoization). As almost always is the case with this type of problems, the solution is easy once you see it. However, in an ordinary SRM, this would be rated as a hard problem. Why it was not a 600 pointer, I don't understand.
Lets try the standard induction approach: given a continuous part of the original strip and the current color this strip has (initially the whole strip has an undefined color), we want to break this down into smaller instances of the same problem. Define this problem like this:
min[left,size,color] = the minimum number of brushes required to paint position
left, left+1, ... , left+size-1 of the original strip,
assuming these position currently has color color.
The desired return value is then simply min[0,stripes.length(),'?'].
It requires one insight to solve this min-problem: the next stroke may always start at the leftmost position unless this position is already in the correct color. If the leftmost position is in the wrong color, we must paint it sooner or later anyway, so why not now? This reasoning only make sense for the leftmost (and rightmost) position, because there is no gain to first paint this position with another color, which may be true of interior positions.
So we first check if the leftmost position is in the wrong color. If it already is in the desired color, we simply return min[left+1,size-1,color] since we then have one less position to worry about. Otherwise we loop over all possible stroke lengths, from 1 to size:
loop i from 1 to size sum = 1 + min[left+1,i-1,stripe[left]] + min[left+i,size-i,color]; update best solution found so far if necessary end loop
The logic is as follows: we make a stroke of color stripe[left] (the color of the leftmost position) from left to left+i-1, inclusive - this accounts for the 1. We then get two subproblems, one part of the strip is in color stripe[left], the other part is in the original color. We solve these subproblems by a recursive call. On the part of the strip which we changed color, we know that the leftmost position is in the correct color, so we can skip ahead one position there (thus explaining the left+1,i-1).
What remains is a terminating case, so we don't recurse forever. That one is simple: if the length of the stripe is zero, it requires no strokes at all.
When implementing this, it's essential that we use memoization, otherwise our solution will time out pretty fast. Memoization should always be considered in a recursive function which doesn't have any side effects, such as changing global variables. A function is a pure mathematical function if it always returns the same value given the same input parameters. Such functions are the only ones memoization can be applied on: if we ever call the function with the same parameters as we've done before, we just look up what answer we got last time instead of evaluating it again. It can be implemented like this:
int memo[50][51][128]; // Initialize to -1 to mark not evaluated
int min(int left, int size, char col)
{
if (memo[left][size][col]>=0) return memo[left][size][col];
// Evaluate function and store result in best
memo[left][size][col]=best;
return best;
}
One can also use dynamic programming to solve the problem. This is basically the same thing, except that instead of the recursive calls, we evaluate the memo table in such an order that the results of recursive calls already has been calculated, like this:
for(int size=0;size<=stripes.length();size++)
for(left=0;left<stripes.length()-size;left++)
for(col='@';col<='Z';col++) {
// Evaluate min[left][size][col] here
}
Notice that in the evaluation of min[left,size,col] the subproblems always had a smaller size than the original problem, so if we evaluate the subproblems starting from size 0 and then working up, these recursive calls can instead be looked up directly from the memo table as we know they have already been evaluated.
And that's it! The hardest part in a problem like this is figuring out the mathematical function and what parameters it should use. Once this is done, it's pretty straightforward. Just remember that the function must be a mathematical one (without side effects), otherwise we can't use memoization.
For an implementation of the recursive approach, see DjinnKahns solution and for a dynamic programming solution, see the solution by ValD.
RoboCourier
Used as: Division-I, Level 3:
Value 1000 Submission Rate 7 / 123 (5.69%) Success Rate 4 / 7 (57.14%) High Score radeye for 604.51 points
Reference implementation: Yarin
Implementation
It's apparent that this is a typical shortest-path problem, albeit a slightly trickier one due to the hexagonal coordinate system and different travelling speeds depending on if it's the first (or last) move in a direction or not.
The first thing to do is to get rid of the annoying hexagonal coordinate system. Or rather, how to translate the 6 hexagonal directions into equivalent directions in a grid world. The following picture shows how this can be done:
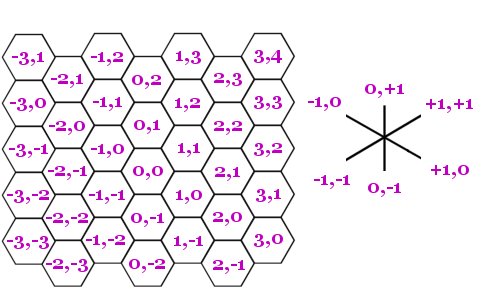
As can be seen, the 6 directions corresponds to movements in x & y coordinates according to the picture to the right. Or, if translated to code, the following constant arrays:
const int dx[6]={0,1,1,0,-1,-1};
const int dy[6]={1,1,0,-1,-1,0};
We can thus easily represent a position in the hexagonal grid using ordinary x,y coordinates.
The next step is to convert the input to an undirected graph. Each node in the graph should correspond to a hexagon that the scout robot has visited, and the edges in the graph should correspond to movements from one hexagon to another by the robot. One can note that each node can have at most 6 edges, one for each possible direction, and there can be at most 501 nodes (for instance, if the scout executes 500 F's). So to represent each node in the graph, we can use the following structure: (C++ code)
struct TNode
{
int x,y; // x and y coordinates of the node
int edge[6]; // Node number to reach if travelling in this direction. -1 if no edge.
};
TNode nodes[501];
int noNodes; // Number of nodes in graph
We create this graph by simulating the movements of the scout robot. Every time the scout moves ahead, we check which node it's at (if it's a new node, we add the information about this nodes coordinate in the structure above) and add the appropriate edge (in both directions!). It might look like this:
int x=0,y=0,dir=0; // Start square
for(int i=0;i<pathConcat.size();i++) {
switch (pathConcat[i]) {
case 'R' : dir=(dir+1)%6; break;
case 'L' : dir=(dir+5)%6; break;
case 'F' :
src=lookup(x,y);
x+=dx[dir];
y+=dy[dir];
dest=lookup(x,y);
nodes[src].edge[dir]=dest;
nodes[dest].edge[(dir+3)%6]=src;
break;
}
}
int start_node=lookup(0,0);
int dest_node=lookup(x,y);
The lookup function simply takes a pair of coordinates and returns which node in the graph has this coordinate pair. If no node has yet been assigned this coordinate pair, we create a new node in the graph:
int lookup(int x, int y) {
for(int i=0;i<noNodes;i++)
if (nodes[i].x==x && nodes[i].y==y) return i;
// Create a new node
for(int i=0;i<6;i++)
nodes[noNodes].edge[i]=-1; // No edges from this new node yet
nodes[noNodes].x=x;
nodes[noNodes].y=y;
return noNodes++;
}
Now we have a nice undirected graph corresponding to legal movements in the graph for our courier robot. All that remains is finding the shortest path from start_node to dest_node. Since turning 60 degrees also takes time (3 seconds), the actual search graph must contain even more nodes (6 times as many), but this graph doesn't have to be built explicitly. Let a state be the complete knowledge of the robots whereabouts: the location and the direction. Imagine creating a new graph with one node for each state - it is in this graph we do the shortest path search. From each state we can either turn 60 degrees clockwise or counter clockwise, or we can move one or more steps in the current direction:
int curNode=state/6,curDir=state%6;
if (dist[curNode*6+(curDir+1)%6]>timeUsed+3)
dist[curNode*6+(curDir+1)%6]=timeUsed+3;
if (dist[curNode*6+(curDir+5)%6]>timeUsed+3)
dist[curNode*6+(curDir+5)%6]=timeUsed+3;
int steps=0;
// Try moving in the current direction until it's not possible
while (nodes[curNode].edge[curDir]>=0) {
steps++;
curNode=nodes[curNode].edge[curDir];
int timeMove=4;
if (steps>1) timeMove=8+(steps-2)*2;
if (dist[curNode*6+curDir]>timeUsed+timeMove)
dist[curNode*6+curDir]=timeUsed+timeMove;
}
One can also build into the state whether or not the robot has started to move, and thus avoid the while-loop in the code above, see SnapDragons solution for an implementation of that version.
